Decision Tree

什么是决策树？

决策树英文全程Decision Tree，其思路在我们生活中很常见，很多时候我们会不自觉的使用这种思路进行一些判断。

举一个例子：假设一个公司想要招聘机器学习算法工程师，那么公司在招聘时可能会采用下面图中的流程。首先看一下应聘者有没有发表过机器学习领域的顶会论文，如果发表过直接录用，没有的话再看一下其背景是否是研究生。不过不是研究生需要看一下其本科成绩是否GPA年纪前10，如果是的话直接录用，否则进行考察。如果是研究生，再进一步看看研究生期间学校参与的项目是否与机器学习相关，如果相关其有机器学习实际应用经验，就直接录用，否则进行考察。

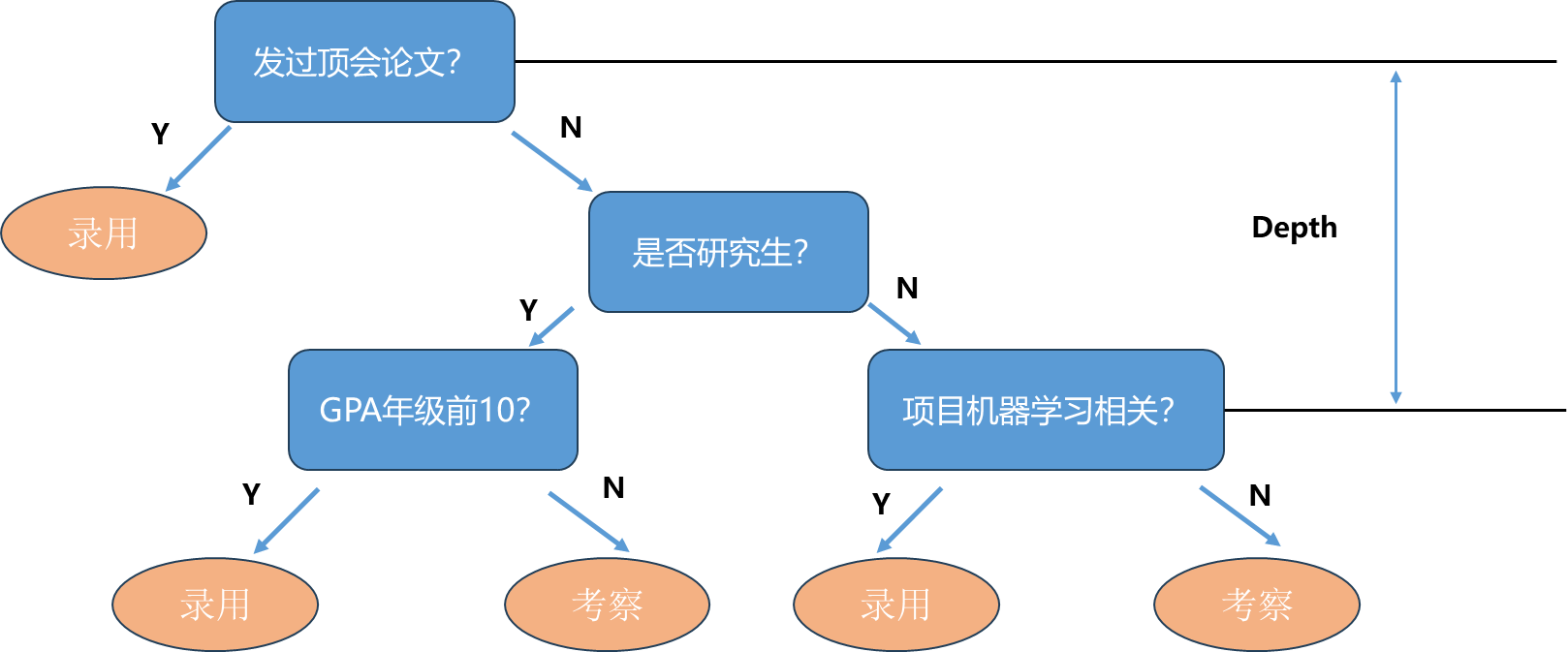
image-20251019135722604

这样的过程形成了一个树的结构，叶子节点位置是我们最终做出的决策，这个决策也可以理解为是对输入应聘者的信息进行了一个分类(录用或后续考察两类)，这样一个过程就叫做决策树。同时整棵树有个深度，上图深度为3，即最多通过3次判断对数据进行相应分类。

上面例子中每个根节点决策时判断这个属性是可以用”Yes"或“No”来回答的问题，实际上真实数据很多内容都是一个具体的数值，那么对于具体的数值决策是如何表征的呢？

先看一下Scikit-learn包装的决策树算法如何进行具体的分类，然后通过分类的结果认识一下决策树这种方法。

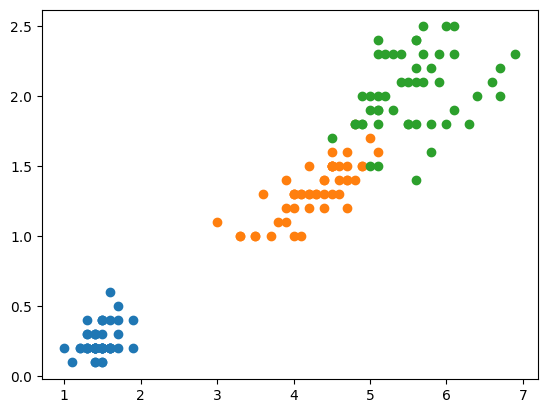
  • 加载iris鸢尾花数据，为了方便可视化只取后两个维度
1
2
3
4
5
6
7
8
9
10
11
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

iris = datasets.load_iris()
X = iris.data[:,2:]
y = iris.target
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.scatter(X[y==2,0], X[y==2,1])
plt.show()

image-20251019151623393

  • 使用scikit-learn封装的decision tree进行分类,传入max_depth=2, criterion=“entropy”
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from sklearn.tree import DecisionTreeClassifier

dt_clf = DecisionTreeClassifier(max_depth=2, criterion="entropy", random_state=42)
dt_clf.fit(X, y)

def plot_decision_boundary(model, axis):
    
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]

    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, cmap=custom_cmap)
plot_decision_boundary(dt_clf, axis=[0.5, 7.5, 0, 3])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.scatter(X[y==2,0], X[y==2,1])
plt.show()

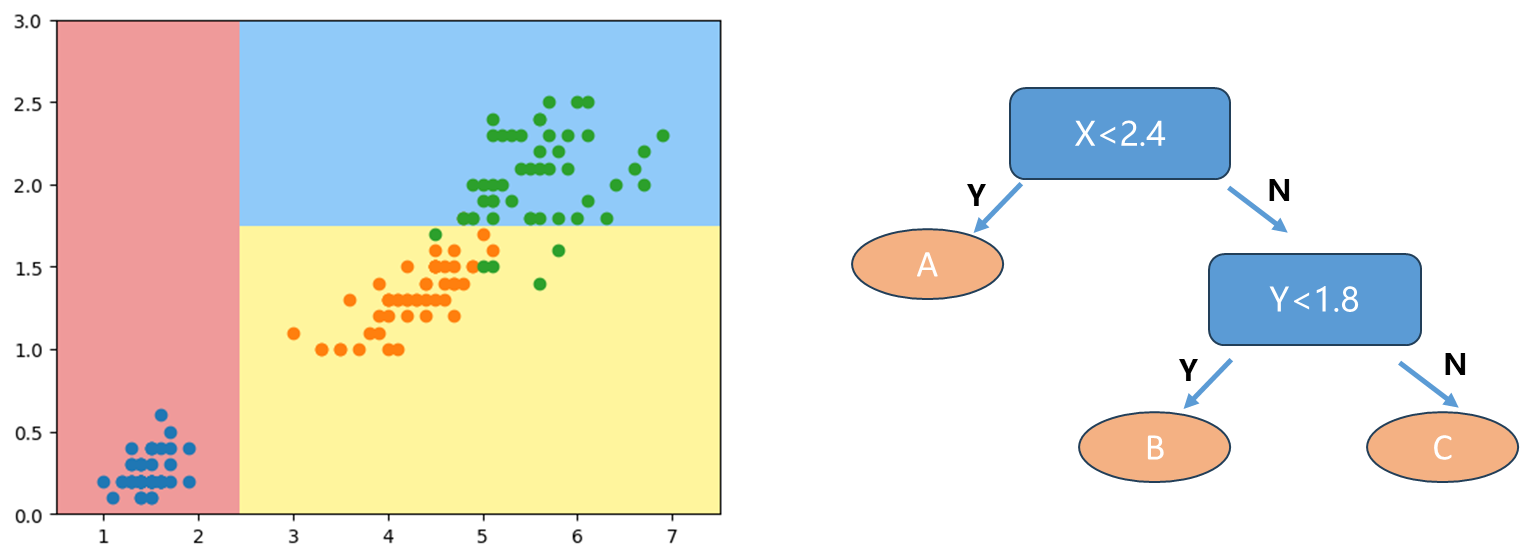
image-20251019152232079

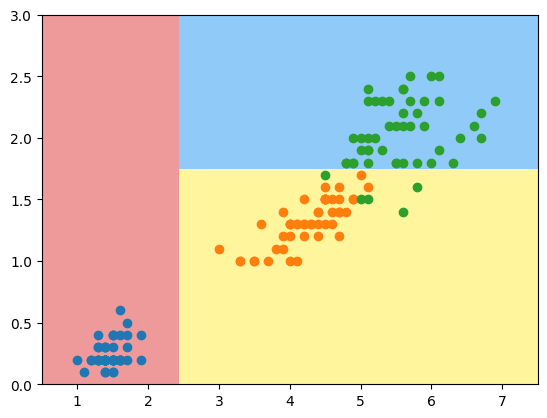
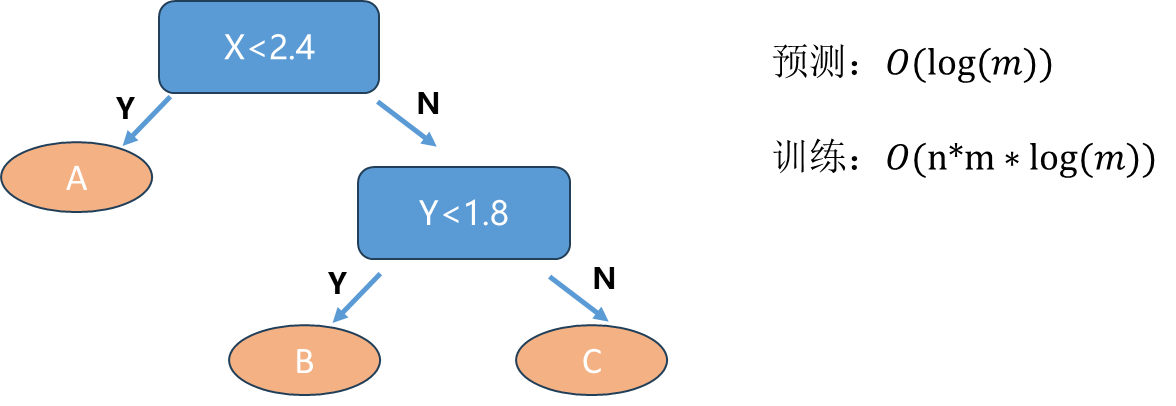
根据我们得到的决策边界绘制一个简单的决策树(右图)，首先这里我们数据的特征都是数字数值特征(X轴，y轴都是数值特征)。如果X<2.4，我们直接分为蓝色的点即A类，否则看Y是否<1.8，是即分为B类即橙色点，否则最后分为C类绿色点。

可见决策树是一个非参数学习算法，可以解决分类问题，和KNN一样可以天然解决多分类问题，而不像Logistic Regression和SVM需要OvR和OvO来解决多分类问题。同时也可以解决回归问题, 比如用落在叶子节点上所有样本的平均值来作为回归问题的预测值。最后决策树还有非常好的可解释性。

信息熵

那么剩下问题就是怎么构建决策树？上面例子数据只有2个维度，如果样本有成百上千个维度，那么每个节点在哪个维度做划分？某个维度在哪个值上做划分(像上面例子中2.4，1.8)？先介绍一下处理这种问题的一个方式-信息熵。

熵在信息论中代表随机变量的不确定度的度量 ，熵越大代表数据的不确定性越高，熵越小代表数据的不确定性越低。

信息熵的计算公式：

H=−∑i=1kpilog(pi)H=-\sum_{i=1}^kp_ilog(p_i)

一个系统中可能有k类的信息， 每一个信息所占的比例就叫做pip_i ，比如iris鸢尾花数据有三种可能每个都占1/3.加上负号是因为log(pi)<0log(p_i)<0 .

计算示例：

SystemA:{13,13,13}H=−13log(13)−13log(13)−13log(13)=1.0986SystemB:{110,210,710}H=−110log(110)−210log(210)−710log(710)=0.8018SystemC:{1,0,0}H=−1log(1)=0System\quad A:\{\frac{1}{3},\frac{1}{3},\frac{1}{3}\} \\ H=-\frac{1}{3}log(\frac{1}{3})-\frac{1}{3}log(\frac{1}{3})-\frac{1}{3}log(\frac{1}{3})\\ =1.0986\\ System\quad B:\{\frac{1}{10},\frac{2}{10},\frac{7}{10}\} \\ H=-\frac{1}{10}log(\frac{1}{10})-\frac{2}{10}log(\frac{2}{10})-\frac{7}{10}log(\frac{7}{10})\\ =0.8018\\ System\quad C:\{1,0,0\} \\ H=-1log(1)=0\\

可见系统A的熵比系统B的熵要大，即系统B比系统A确定性更高。极端一些如系统C的信息熵为0，数据全在一类中，最确定。

如果是二分类问题, 信息熵公式：

H=−xlog(x)−(1−x)log(1−x)H=-xlog(x)-(1-x)log(1-x)

绘制一下此时曲线：

1
2
3
4
5
6
7
8
9
import numpy as np
import matplotlib.pyplot as plt

def entropy(p):
    return -p * np.log(p) - (1-p) * np.log(1-p)
    
x = np.linspace(0.01, 0.99, 200)
plt.plot(x, entropy(x))
plt.show()

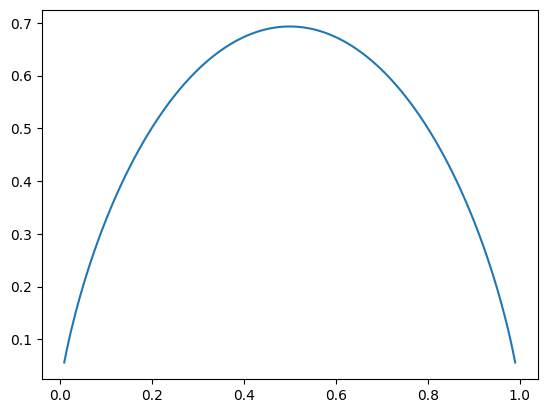
image-20251019175436003

可以发现x取0.5时，即两个类别各占1/2，此时熵取到最大值，此时确定性是最低的。同时无论x变小或者变大，信息熵都在降低，因为代表着更倾向某一类，确定性变高了。

回到前面两个问题，我们的目标就很明确了，在每个节点的某个维度的某个取值下，根据这个维度取值对数据划分后使得系统的信息熵降低。

模拟用信息熵寻找最优划分

信息熵可以看到当前数据的不确定度。对于决策树来说，根节点相当于拥有全部的数据，在根节点的基础上找到一个维度一个阈值对根节点进行划分，划分以后希望数据整体信息熵是降低的，进而对划分出来的节点可以再用同样的方式寻找特定的维度和阈值进行划分，使得整体信息熵继续减少，这样的过程递归下去就形成了决策树。

编程模拟：

  • 首先数据依旧采用iris鸢尾花数据，方便可视化取后两个特征(代码同上面)

  • 根据维度和阈值划分的Split函数

1
2
3
4
def split(X, y, d, value):
    index_a = (X[:,d] <= value)
    index_b = (X[:,d] > value)
    return X[index_a], X[index_b], y[index_a], y[index_b]

其中dd 和valuevalue 代表划分的维度和阈值，最终返回划分的结果。

  • 寻找最优dd 和valuevalue 的try_split函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
from collections import Counter
from math import log

def entropy(y):  # 计算信息熵函数
    counter = Counter(y)
    res = 0.0
    for num in counter.values():
        p = num / len(y)
        res += -p * log(p)
    return res

def try_split(X, y):
    
    best_entropy = float('inf')  # 初始化 信息熵
    best_d, best_v = -1, -1  # 初始化维度 和 阈值
    for d in range(X.shape[1]):  # 遍历 所有的 维度
        sorted_index = np.argsort(X[:,d]) 
        for i in range(1, len(X)):  # 遍历 每个样本
            if X[sorted_index[i], d] != X[sorted_index[i-1], d]:
                v = (X[sorted_index[i], d] + X[sorted_index[i-1], d])/2 # 两个相邻样本中间值 为阈值
                X_l, X_r, y_l, y_r = split(X, y, d, v)
                p_l, p_r = len(X_l) / len(X), len(X_r) / len(X)
                e = p_l * entropy(y_l) + p_r * entropy(y_r) # 计算 信息熵
                if e < best_entropy:
                    best_entropy, best_d, best_v = e, d, v
                
    return best_entropy, best_d, best_v

try_split函数输入为当前节点的XX 和yy ，算法具体流程是遍历当前数据的每一个维度，然后在该维度上寻找最优的阈值，每次以相邻两个样本值的中间值作为 划分阈值。

  • 调用上面算法
1
2
3
4
best_entropy, best_d, best_v = try_split(X, y)
print("best_entropy =", best_entropy)
print("best_d =", best_d)
print("best_v =", best_v)

得到第一次划分结果：

best_entropy=0.462best_d=0best_v=2.45best\_entropy = 0.462\\ best\_d = 0\\ best\_v = 2.45

可以发现在第0个维度阈值为2.45的位置进行划分使得信息熵最低。接着根据上面的结果得到第一次划分后的数据：

image-20251019214304637

可以发现左边数据信息熵为0，右边数据信息熵为0.69.

  • 此时完成了第一次划分，左边数据信息熵为0，不要划分了，接着对右边数据继续第二次划分
1
2
3
4
best_entropy2, best_d2, best_v2 = try_split(X1_r, y1_r)
print("best_entropy =", best_entropy2)
print("best_d =", best_d2)
print("best_v =", best_v2)

得到右边数据第二次划分结果：

best_entropy=0.215best_d=1best_v=1.75best\_entropy = 0.215\\ best\_d = 1\\ best\_v = 1.75

可以发现此时在第1个维度阈值为1.75的位置进行划分使得信息熵最低，第二划分后左边数据信息熵为0.3，右边数据信息熵为0.104.此时信息熵没有降到0，可以接着往深处划分。

image-20251019214541334
  • 根据上面的划分结果对比一下最开始我们使用scikit-learn划分的结果图：

image-20251019214700500

可以发现我们模拟结果：第0个维度阈值为2.45的位置，第1个维度阈值为1.75的位置,这两个结果与上图基本一致。

基尼系数

前面介绍的是采用信息熵的方式对决策树进行划分，其实还可以使用另外一个指标对决策树进行划分，即基尼系数。基尼系数的计算比信息熵简单很多：

G=1−∑i=1kpi2G=1-\sum_{i=1}^kp_i^2

这个式子和上面信息熵的式子具有同样的性质，同样假设数据有三个类别，计算示例如下：

SystemA:{13,13,13}G=1−(13)2−(13)2−(13)2=0.6666SystemB:{110,210,710}G=1−(110)2−(210)2−(710)2=0.46SystemC:{1,0,0}G=1−12=0System\quad A:\{\frac{1}{3},\frac{1}{3},\frac{1}{3}\} \\ G=1-(\frac{1}{3})^2-(\frac{1}{3})^2-(\frac{1}{3})^2\\ =0.6666\\ System\quad B:\{\frac{1}{10},\frac{2}{10},\frac{7}{10}\} \\ G=1-(\frac{1}{10})^2-(\frac{2}{10})^2-(\frac{7}{10})^2\\ =0.46\\ System\quad C:\{1,0,0\} \\ G=1-1^2=0\\

同样可见系统A的熵比系统B的熵要大，说明系统B比系统A确定性更高。极端一点如系统C，此时信息熵为0，数据全在一类中，最确定。因此基尼系数和信息熵一样可以作为数据不确定性的度量。

同样如果是二分类问题, 基尼系数公式：

G=1−x2−(1−x)2=−2x2+2xG=1-x^2-(1-x)^2\\=-2x^2+2x

可以看出此时是一个抛物线，在x=1/2x=1/2 取到极大值.即两个类别各占1/2，此时基尼系数取到最大值，此时确定性是最低的，同时无论x变小或者变大，基尼系数都在降低，因为代表着更偏斜某一类，确定性变高了。这里也与采用信息熵时的结果一致。

编程示例：

  • 同样采用与上面一致的鸢尾花iris数据，先使用scikit-learn库的决策树进行分析,注意令criterion="gini"即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

iris = datasets.load_iris()
X = iris.data[:,2:]
y = iris.target
from sklearn.tree import DecisionTreeClassifier

dt_clf = DecisionTreeClassifier(max_depth=2, criterion="gini", random_state=42)
dt_clf.fit(X, y)

def plot_decision_boundary(model, axis):
    
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*200)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*200)).reshape(-1, 1),
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]

    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, cmap=custom_cmap)
    
plot_decision_boundary(dt_clf, axis=[0.5, 7.5, 0, 3])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.scatter(X[y==2,0], X[y==2,1])
plt.show()

image-20251019222154493

可以发现这个决策边界结果与使用信息熵是相同的。

  • 接下来同样模拟使用基尼系数划分，代码同上面模拟信息熵基本一致，只是将信息熵计算修改为了基尼系数计算。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from collections import Counter
from math import log

def split(X, y, d, value):
    index_a = (X[:,d] <= value)
    index_b = (X[:,d] > value)
    return X[index_a], X[index_b], y[index_a], y[index_b]

def gini(y):
    counter = Counter(y)
    res = 1.0
    for num in counter.values():
        p = num / len(y)
        res -= p**2
    return res

def try_split(X, y):
    
    best_g = float('inf')
    best_d, best_v = -1, -1
    for d in range(X.shape[1]):
        sorted_index = np.argsort(X[:,d])
        for i in range(1, len(X)):
            if X[sorted_index[i], d] != X[sorted_index[i-1], d]:
                v = (X[sorted_index[i], d] + X[sorted_index[i-1], d])/2
                X_l, X_r, y_l, y_r = split(X, y, d, v)
                p_l, p_r = len(X_l) / len(X), len(X_r) / len(X)
                g = p_l * gini(y_l) + p_r * gini(y_r)
                if g < best_g:
                    best_g, best_d, best_v = g, d, v
                
    return best_g, best_d, best_v
  • 第一次划分结果
image-20251019222527469

可以发现在第0个维度阈值为2.45的位置进行划分使得信息熵最低为0.333。可以发现左边数据基尼系数为0，右边数据基尼系数为0.5.

  • 第二次划分
image-20251019222658298

可以发现在第1个维度阈值为1.75的位置进行划分使得信息熵最低为0.11。可以发现左边数据基尼系数为0.16，右边数据基尼系数为0.04.

简单对信息熵和基尼系数做个对比：

  • 首先从计算式子来看，信息熵计算(要计算log非线性函数)比基尼系数稍慢。因此scikit-learn默认为基尼系数。
  • 从结果来看，两者大多时候没有特别的效果优劣之分

CART和决策树超参数

决策树通常还有一个名字叫做CART即Classification And Regression Tree， 从名字也能发现决策树既能解决分类问题也能解决回归问题.这种决策树的特点就是根据某一个维度dd 和 某一个阈值vv 进行二分，这样得到的决策树是一个二叉树，这样的二叉树通常可以叫做CART.

Scikit-learn库实现的决策树也都是CART方式的决策树.但还有一些其它创建决策树的方法比如ID3、C4.5、C5.0.

对于建立好的决策树，其做预测的复杂度是O(log(m))O(log(m)) 的级别，m是样本个数，平均来看每次在一个节点上划分都是对当前数据集进行对半划分，所以这棵树最终高度是log(m)log(m) .而其寻来你复杂度是O(n∗m∗log(m))O(n*m*log(m)) 的级别, 因为构建每个节点时需要对每个样本每个维度进行遍历，相对较高。

image-20251019224044937

更重要的是决策树非常容易产生过拟合，同KNN算法一样.因此我们实际创建决策树时需要对决策树进行剪枝来降低复杂度解决过拟合。

编程示例：

  • 加载数据: 这里采用生成的非线性虚拟数据，这样可以更好看出来决策树发生过拟合的样子以及使用超参数解决过拟合产生的结果。
1
2
3
4
5
6
7
8
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

X, y = datasets.make_moons(noise=0.25, random_state=666)
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()

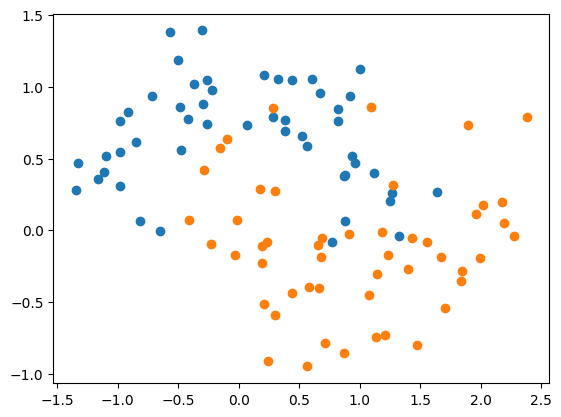
image-20251019224937011

  • 先使用sklearn的决策树进行训练，但是不限定max_depth参数.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from sklearn.tree import DecisionTreeClassifier

dt_clf = DecisionTreeClassifier()
dt_clf.fit(X, y)

def plot_decision_boundary(model, axis):
    
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]

    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
plot_decision_boundary(dt_clf, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()

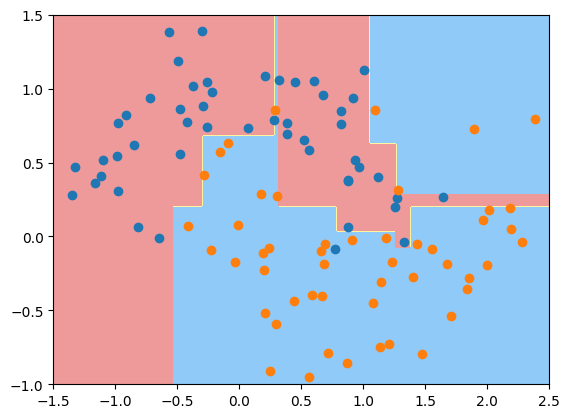
image-20251019225047431

可以发现决策边界很不规则，明显此时产生了过拟合现象。

  • 尝试传入不同的超参数看看如何抑制过拟合现象
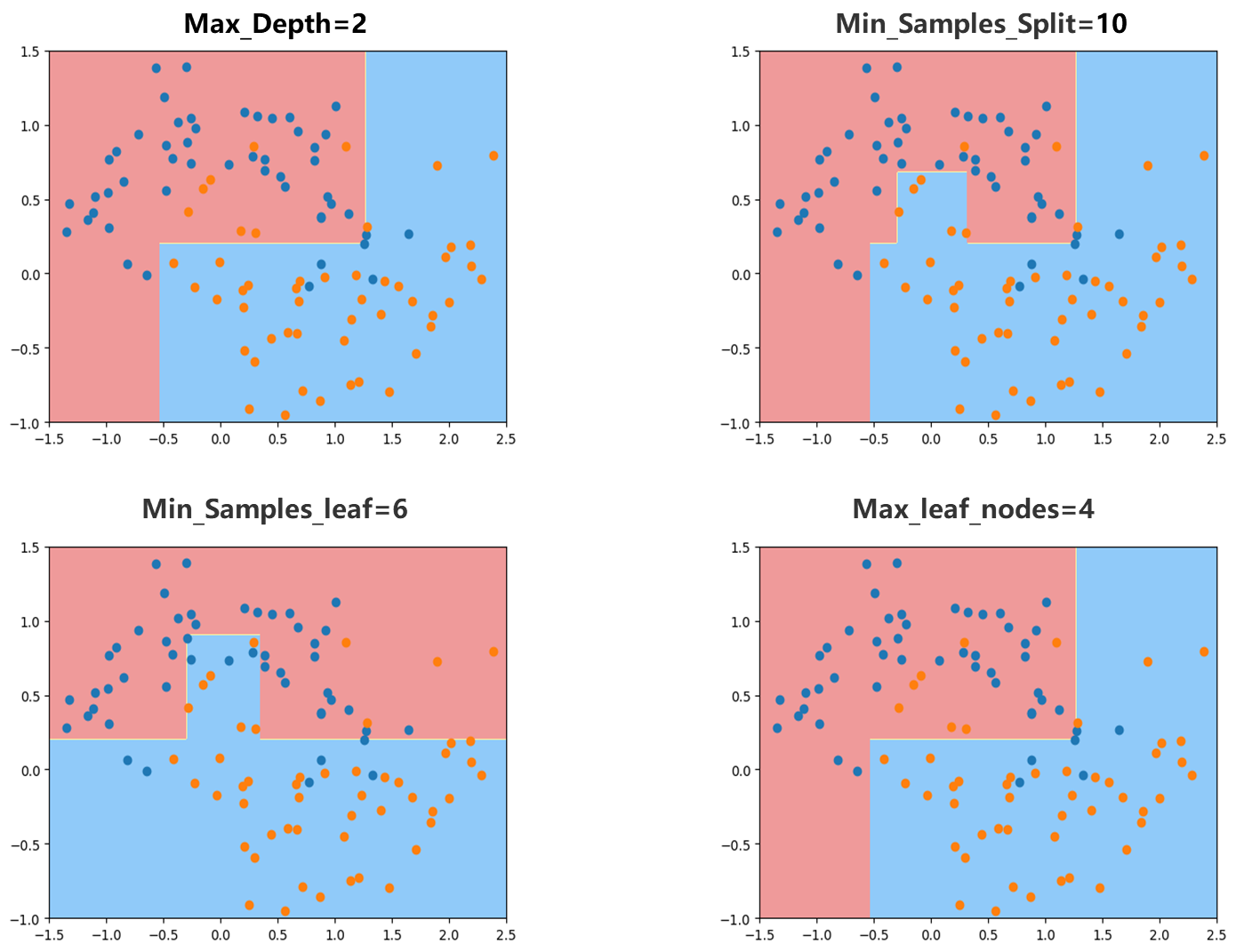
image-20251019225757227
  • 传入max_depth=2，显然不在过拟合，边界很清晰
  • 传入min_samples_split=10，这个参数表示一个节点至少要有多少样本数据才对这个节点进行拆分，可以发现这个决策边界过拟合程度也很低，显然这个值越高越不容易过拟合，但太高会欠拟合。
  • 传入min_samples_leaf=6，这个参数表示一个叶子节点至少要有多少样本数据，可以发现这个决策边界也一定程度遏制了过拟合现象。
  • 传入max_leaf_nodes=4，这个参数表示最多有几个叶子节点，对于决策树来说叶子节点越多决策树越复杂越容易产生过拟合现象。可以发现这个决策边界也一定程度遏制了过拟合现象。

可以发现使用这几个超参数赋予不同的值相应的结果都比原本好，解决了过拟合的问题。但实际使用这些参数也需要注意首先也要避免欠拟合，其次这些参数可以互相组合网格搜索来找到比较好的超参数。

实际上决策树本身做分类还是回归效果都不会特别的好，决策树有一定的局限性。但尽管如此决策树依然非常有用，随机森林就使用了决策树的思路。

决策树解决回归问题

决策树的思想可以非常容易解决回归问题，当使用CART方式将决策树建立出来之后，每一个叶子节点都包含了若干数据，如果这些数据相应输出值是类别的话那么我们就可以在叶子节点中让这些数据进行投票，哪个类别的数据多我们就样本进入这个子节点归为这个类别。如果数据输出是一个具体的数值，即回归问题解决的问题，当一个新样本点来到决策树来到某一个叶子节点，就可以用叶子节点数据输出值平均值作为预测结果。

scikit-learn示例：

  • 加载boston房价数据
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import pandas as pd
import numpy as np

data = pd.read_csv("BostonHousing.csv")
X = data.iloc[:,:13]
y = data.iloc[:,13]

filter_condition=y<50
x_filtered=X[filter_condition]
y_filtered=y[filter_condition]
nan_mask=x_filtered.isnull().any(axis=1)| y_filtered.isnull()
x_clean= x_filtered[~nan_mask]
y_clean=y_filtered[~nan_mask]
X_array = np.array(x_clean)
y_array = np.array(y_clean)

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
  • 使用默认参数回归
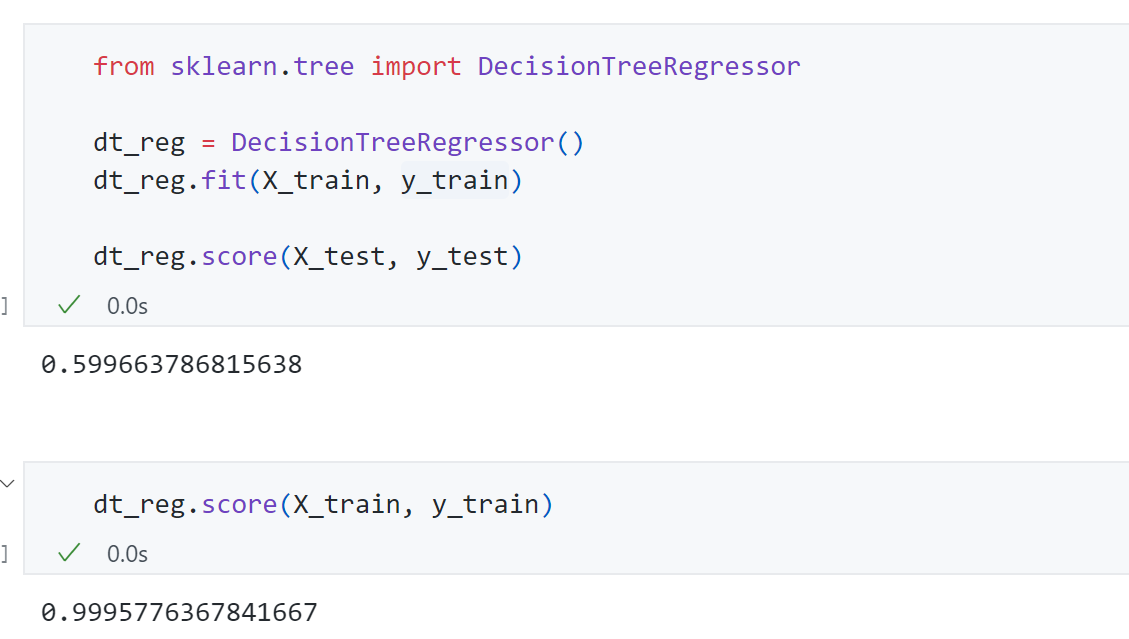
image-20251019231743715

最终得到测试集score为0.59，训练集score为0.99，说明此时过拟合，可以通过调参来解决。

决策树局限性

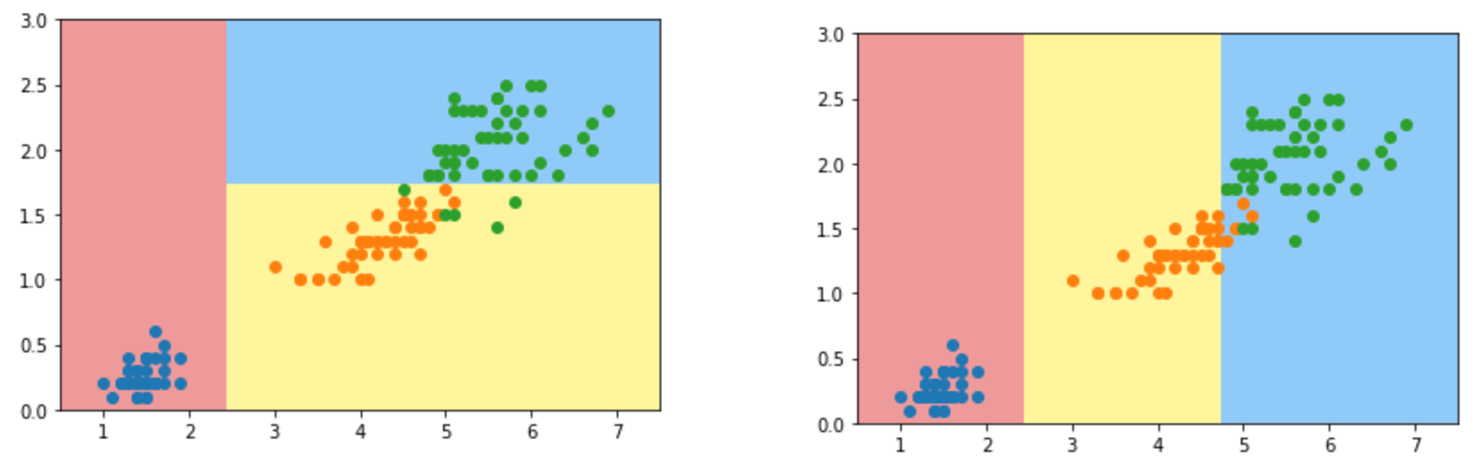
决策树最大局限性从上面鸢尾花数据的决策边界图就可以看出来了，即决策边界是横平竖直的，因为我们每一次划分都是沿着这个维度>一个阈值或小于这个阈值，必然这个边界会平行于这个轴。

image-20251019152232079

举个例子：我们使用决策树可能会是下面左图的决策边界，但实际右图的决策边界应该是实际情况。

image-20251019233853660

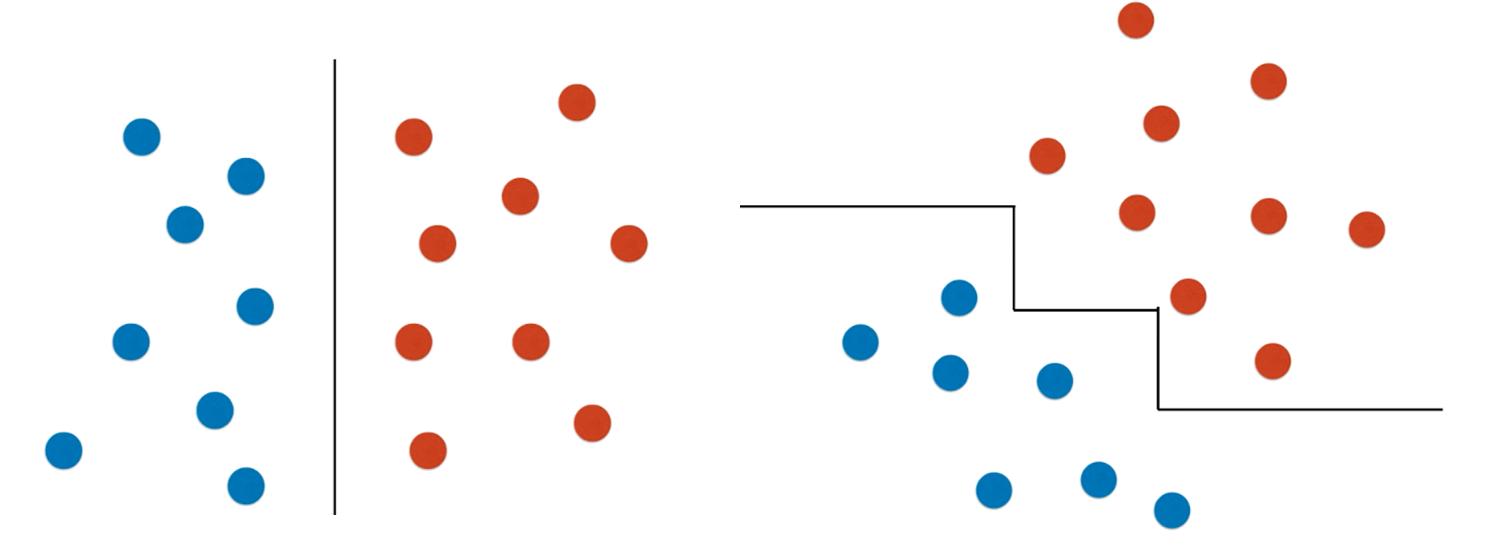
再举个例子：假设数据集是左图的样子，那么可以用决策树用一条直线很好的划分出来；但如果数据分布不变稍微旋转成右边的样子，那么决策树得到的边界可能就变成了一个阶梯状的样子而不是一条直线。

image-20251019234218150

另外一个局限性就是决策树对个别样本点很敏感：左图是原本决策树的决策边界，然后删掉了原数据的一个样本点，决策边界就变成了右图的样子。

image-20251019234818696

总的来说，决策树有两个比较重要的局限性：

  • 生成的决策边界横平竖直的，如果数据产生了一点偏斜，决策树得到的结果就不能很好反映数据的分布情况。
  • 作为一个非参数学习算法，对个别样本点非常敏感。

但决策树本身还是一个非常有用的机器学习算法，主要用处并不是单独进行使用，更重要的一个应用是使用集成学习的方式创建一种随机森林的算法。