Insertion Sort
插入排序
插入排序法也是我们生活中常用的一种排序算法. 以扑克牌为例,当我们斗地主抓了一手牌,我们需要对这一手牌进行排序,这个排序过程大多数人通常都使用的是插入排序法。
以数字代替扑克牌为例,插入排序的过程:
867109687109678109678109678910
- 初始的五张牌是
8 6 7 10 9,通常我们从左向右一张一张牌的看去整理有序
- 首先8在第一张牌位置不用动,接着看6,发现6比8小,于是交换6和8得到
6 8 7 10 9
- 接着看下一张牌7,发现7比8小,比6要大,于是把7插入到6和8之间得到
6 7 8 10 9
- 接着看下一张牌10,发现其比8大,不动
- 接着看下一张牌9,发现9比10要小,比8要大,于是把9插入到8和10之间得到
6 7 8 9 10
整个过程中,每次只处理一张牌,把这张牌插入到前面已经排好序的牌中。这也是插入名字的由来。
以计算机数组表示为例模拟插入排序:

- 用红色索引
i 指向当前处理的元素,初始指向索引为0的位置即数字6
- 6不需要插入到任何位置,因此红色索引
i++ ,指向数字4,此时需要判断4是否要插入前面元素某一个位置
- 引入蓝色索引
j ,蓝色索引初始指向4所在的位置,然后看j-1的位置 发现是6>4,因此交换4和6同时蓝色索引j 跟着来都j=0 的位置,此时j 前面没有索引了,插入完成。
- 接着红色索引
i++ ,指向数字2,同样为了判断2是否要插入前面元素的某一个位置引入蓝色索引j初始指向2所在的位置,此时j-1 位置是6>2,那么2应该插入到6的前面于是2和6交换位置。此时蓝色索引j=1
- 接着看新的
j-1 位置是4>2,那么2应该插入到4的前面于是2和4交换位置,此时蓝色索引j=0,插入完成
- 后续步骤类似,在此省略描述
这里插入排序法的循环不变量和之前的选择排序法的循环不变量是一致的,那么两者区别在哪?同样处理完四个元素之后,插入排序法的元素是下面一行黄色高亮,选择排序的元素是上面一行黄色高亮。

-
选择排序法完成了4轮循环之后,前面四个元素一定是整个数组中最小的4个元素即1 2 3 4,即对于选择排序算法来说,每处理完一个位置之后,这个位置存放的就是当整个数组全部排序完毕以后这个位置应该存在的元素是谁。
-
插入排序不同,插入排序每次只处理当前的元素,把当前的这个元素放到合适的位置,所以对于插入排序法来说,它永远不会操作i这个索引还没有遍历到的元素,因此插入排序4轮循环处理的是原本数组的前四个元素,它不是最终排序好的结果。
实现插入排序
根据上面算法思路,java代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| public class Insertion_Sort {
private Insertion_Sort(){}
public static <E extends Comparable<E>> void sort(E[] arr){
for(int i = 0; i < arr.length; i++){
for(int j = i; j >= 1 ; j--){
if(arr[j].compareTo(arr[j-1]) < 0)
swap(arr, j, j-1);
else break;
}
}
}
private static <E extends Comparable<E>> void swap(E[] arr, int i, int j){
E temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void main(String[] args) {
int[] dataSize = {10000, 100000};
for(int n:dataSize){
Integer[] arr = ArrayGenerator.generateRandomArray(n, n);
SortingHelper.sortTest("InsertionSort", arr);
}
}
}
|

这里测试代码同上篇“选择排序”,可见n=10000 用时0.087533s ,当n=100000 用时10.644478s . 数据规模n扩大了10倍,但是耗时扩大了100多倍,再次侧面反映 插入排序的时间复杂也是O(n2) 的级别.
这里代码还能进一步做一点优化:
1
2
3
4
5
6
7
8
9
10
11
12
|
public static <E extends Comparable<E>> void sort(E[] arr){
for(int i = 0; i < arr.length; i++){
for(int j = i; j >= 1 ; j--){
if(arr[j].compareTo(arr[j-1]) < 0)
swap(arr, j, j-1);
else break;
}
}
}
|
这里 面如果if(arr[j].compareTo(arr[j-1]) < 0)不满足,那么就直接break.相当于if条件本身即是循环继续执行的条件.同时 j >= 1也是循环继续执行的条件,两者可以合并。
因此优化后如下:
1
2
3
4
5
6
7
8
9
10
|
public static <E extends Comparable<E>> void sort(E[] arr){
for(int i = 0; i < arr.length; i++){
for(int j = i; j >= 1 && arr[j].compareTo(arr[j-1]) < 0; j--){
swap(arr, j, j-1);
}
}
}
|
插入排序小优化
前面实现插入排序的大致过程如下:
246315243615234615
比如当红色索引i 指向元素3时,此时数组顺序为第一行 2 4 6 3 1 5;接着需要开始比较3和6,因为6>3,执行一次交换为第二行 2 4 3 6 1 5;接着比较3和4,因为4>3,在执行一次交换得到第三行2 3 4 6 1 5. 而由交换函数swap的代码可知,每次交换是三次操作.
那么这里能进行化简吗?仔细观察最终结果 2 3 4 6 1 5 是原来基础上 2 4 5 3 1 5 中的 4 6向右平移了一位.这个平移的过程可以只靠一次赋值操作完成,最终知道数字3应该索引为1的位置,在把3这个元素放到这个位置即可.
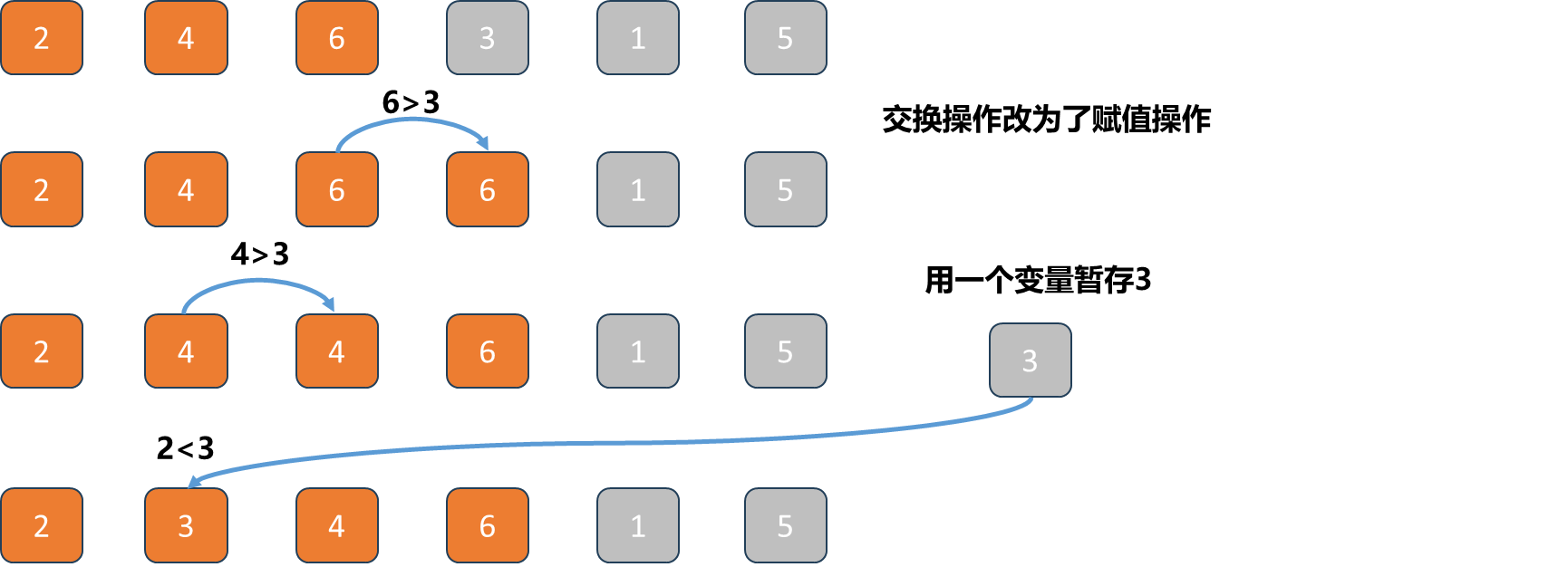
上面整个过程中,每一次操作只用到一次了赋值,而不是交换(一次交换对应三次操作).这样就对插入排序进行了一个小的优化,不过这个小的优化不是时间复杂度上的优化,依旧是一个O(n2) 级别的算法.
编程实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
| public static <E extends Comparable<E>> void sort2(E[] arr){
for(int i = 0; i < arr.length; i++){
E temp = arr[i];
int j;
for(j = i; j>=1 && temp.compareTo(arr[j-1])<0; j--)
arr[j] = arr[j-1];
arr[j] = temp;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| import java.util.Arrays;
public class Insertion_Sort {
private Insertion_Sort(){}
public static <E extends Comparable<E>> void sort(E[] arr){
for(int i = 0; i < arr.length; i++){
for(int j = i; j>=1 && arr[j].compareTo(arr[j-1])<0; j--)
swap(arr,j,j-1);
}
}
public static <E extends Comparable<E>> void sort2(E[] arr){
for(int i = 0; i < arr.length; i++){
E temp = arr[i];
int j;
for(j = i; j>=1 && temp.compareTo(arr[j-1])<0; j--)
arr[j] = arr[j-1];
arr[j] = temp;
}
}
private static <E extends Comparable<E>> void swap(E[] arr, int i, int j){
E temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void main(String[] args) {
int[] dataSize = {10000, 100000};
for(int n:dataSize){
Integer[] arr = ArrayGenerator.generateRandomArray(n, n);
Integer[] arr2 = Arrays.copyOf(arr, arr.length);
SortingHelper.sortTest("InsertionSort", arr);
SortingHelper.sortTest("InsertionSort2", arr2);
}
}
}
|

可以发现InsertionSort2 即优化后的算法要比未优化的算法InsertionSort 前要快一些. 但是这个优化显然是一个常数级别的优化,没有让插入排序的复杂度O(n2) 发生根本的改变,对于一些更高级的排序算法复杂度有一个质上的提升,对于100k或1M级别的数据都可以在1s内完成排序,因此学习算法更多主要精力要在复杂度级别的优化上而不是这种常数级别的优化.
时间复杂度分析
1
2
3
4
5
6
7
8
9
10
11
12
13
| public static <E extends Comparable<E>> void sort2(E[] arr){
for(int i = 0; i < arr.length; i++){
E temp = arr[i];
int j;
for(j = i; j>=1 && temp.compareTo(arr[j-1])<0; j--)
arr[j] = arr[j-1];
arr[j] = temp;
}
}
|
外层for循环从0到n, 内层for循环最坏情况每次从1到i 即0+1+2+..n−1=n∗(n−1)/2 .因此时间复杂度为O(n2) ,这个分析结果也与我们上面代码的性能测试结果一致.
插入排序算法特性
插入排序法有一个非常重要的特性是和选择排序法不同的. 插入排序的终止条件除了j>=1 还有另外一个条件temp.compareTo(arr[j-1])<0 ,如果>0 整个循环就结束了,即插入排序存在一个内层循环提前终止的机制.这个提前终止的机制意味着内层循环不一定要遍历从i到1这么多轮.
举一个比较极端的例子,如果待排序数组本身就是有序的 :
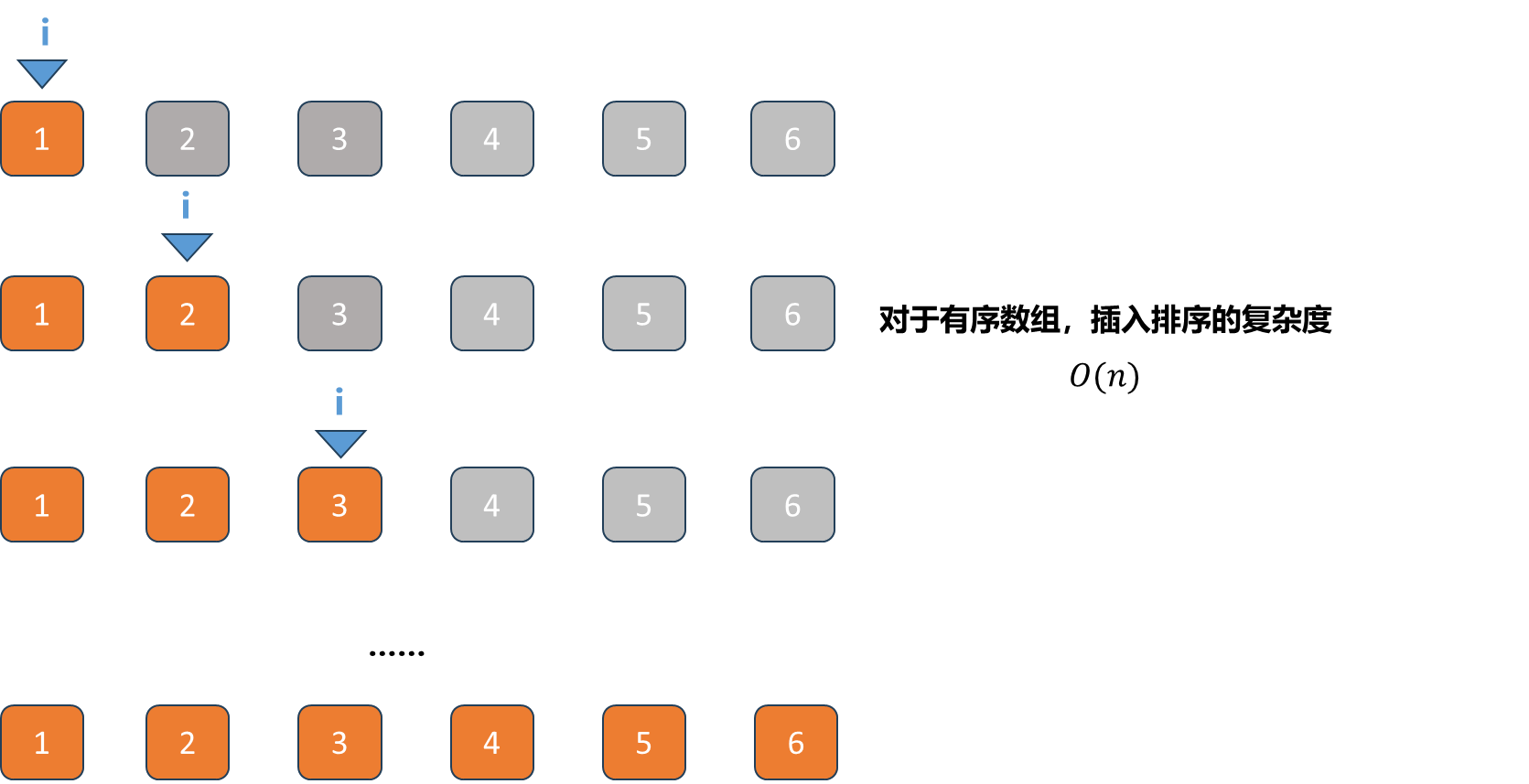
此时插入排序复杂度变成了O(n) 级别. 但对于选择排序来说,总要扫描后面所有未排序的数组来找到最小的元素,即使第一个元素已经是最小的元素.因此选择排序是一个稳定O(n2) 级别的算法.
插入排序这个特点本身也是非常重要的. 如果给你的数据是近乎有序的,即大部分有序的,只有几个数据是无序的,比如银行业务处理的数据,此时使用插入排序算法是一个更好的选择,因为插入排序算法对于有序的数组时间复杂度变成了O(n) 级别,对于近乎有序的数据是同理的.
对于完全有序的数组,插入排序成为O(n)的算法.
插入排序vs选择排序
接下来使用插入排序和选择排序分别针对有序和无序的数组进行性能测试.
测试代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| import java.util.Arrays;
public class InsertionSort {
private InsertionSort(){}
public static <E extends Comparable<E>> void sort(E[] arr){
for(int i = 0; i < arr.length; i ++){
E t = arr[i];
int j;
for(j = i; j - 1 >= 0 && t.compareTo(arr[j - 1]) < 0; j --){
arr[j] = arr[j - 1];
}
arr[j] = t;
}
}
private static <E extends Comparable<E>> boolean isSorted(E[] arr){
for(int i = 1; i < arr.length; i ++)
if(arr[i - 1].compareTo(arr[i]) > 0)
return false;
return true;
}
public static void main(String[] args){
int[] dataSize = {10000, 100000};
for(int n: dataSize){
System.out.println("Random Array : ");
Integer[] arr = ArrayGenerator.generateRandomArray(n, n);
Integer[] arr2 = Arrays.copyOf(arr, arr.length);
SortingHelper.sortTest("InsertionSort", arr);
SortingHelper.sortTest("SelectionSort", arr2);
System.out.println();
System.out.println("Ordered Array : ");
arr = ArrayGenerator.generateOrderedArray(n);
arr2 = Arrays.copyOf(arr, arr.length);
SortingHelper.sortTest("InsertionSort", arr);
SortingHelper.sortTest("SelectionSort", arr2);
System.out.println();
}
}
}
|
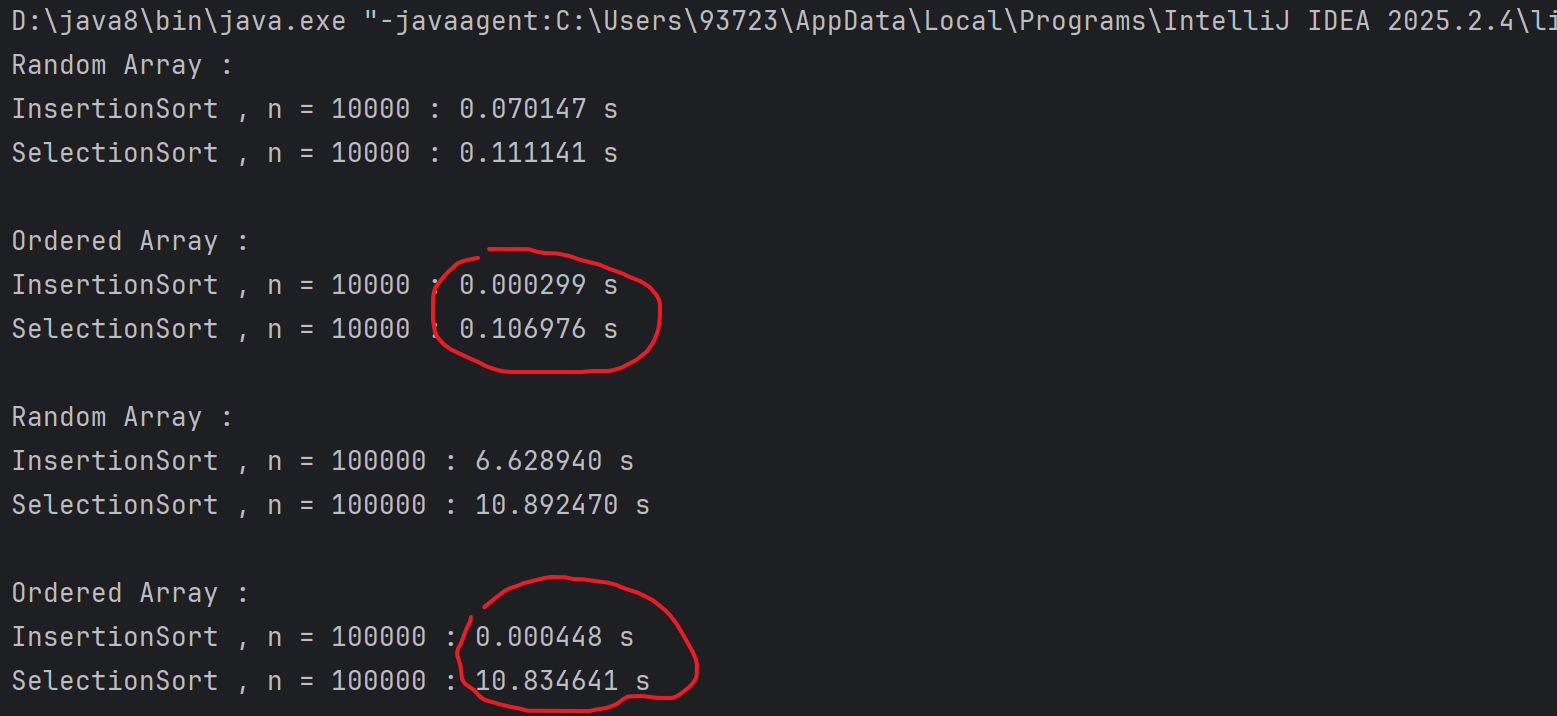
观察上面结果可以发现n=10000 时,对于完全随机的数组Random Array,两种排序耗时相差不大.而对于Ordered Array,插入排序只有0.000299s,而选择排序依然是0.106976s. 对于选择排序不论什么样的数组算法复杂度都是O(n2) .
当n=100000 时,对于Random Array,插入排序是6.6s,选择排序是10.89s,相差不是很大. 对于Ordered Array,插入排序只有0.000448s,而选择排序依然是10.83s. 再次验证了上面的结论.











