线性代数

Matrix

什么是矩阵

矩阵就是看起来平淡无奇的一组数, 通常将这组数字排成m行n列. 如果说向量是对数的拓展，一个向量表示一组数.那么矩阵就是对向量的拓展, 一个矩阵表示一组向量.
$$
\begin {pmatrix}
1 & 2 & 3 & 4\
5 & 6 & 7 & 8\
9 & 10 & 11 & 12\
13 & 14 & 15 & 16\
\end {pmatrix}
\begin {pmatrix}
1 & 2 & 3 & 4\
5 & 6 & 7 & 8\
9 & 10 & 11 & 12\
\end {pmatrix}
$$
如果矩阵表示一组向量，那么就有一个问题：这个矩阵表示的是怎样一组向量？这组向量一共有几个向量？每个向量分别是谁？对于这个问题，由于我们看待矩阵的视角不一样或者应用矩阵的应用场景不一样，我们通常会有不同的看待方式. 如果以宽泛的视角看待这个问题也非常容易，简而言之有两个视角，一个是视角是一行一行的看待这个矩阵，这个矩阵是由4个行向量组成的；另一个视角就是列向量，一列一列的看待.

对于上面的矩阵(左1)，我们可以说是一个$44$ 的矩阵即4行4列. 如果行数和列数不相等(右1),可以说是一个34的矩阵即3行4列. 通常对于这种行数和列数相等的矩阵，我们称之为方阵. 而方阵有很多特殊的性质，有很多特殊性质的矩阵是方阵.

在通常数学符号体系中，我们使用大写字母比如A来代表一个矩阵，矩阵的每一个元素通常用和这个大写字母相对应的小写字母比如a来表示，用小写字母下标来表示这个元素对应的行数和列数.比如$a_{ij}$ 代表这个元素在A矩阵的第i行和第j列.
$$
A=\begin {pmatrix}
a_{11} & a_{12} & a_{13} & a_{14}\
a_{21} & a_{22} & a_{23} & a_{24}\
a_{31} & a_{32} & a_{33} & a_{34}\
\end {pmatrix}
$$
线性代数中表示矩阵是和计算机中的二维数组表示是一样的.

举一个比较常见的矩阵例子：
$$
语文\quad数学\quad 英语\
A=\begin {pmatrix}
86 & 82 & 92 \
73 & 97 & 84 \
92 & 72 &93 \
\end {pmatrix}
\begin{array}{c}
Dong \
Liu \
Wang
\end{array}
$$
我们常见的成绩单，每一个元素都表示一个成绩，整个矩阵表示一个班级若干个同学各个科目的成绩，每一行表示每个同学不同科目的成绩， 每一列表示这个科目这三个同学在的成绩. 我们可以对行向量求和得到每个同学的总分，也可以列向量求平均得到这个班级该科目的平均分.

这是数据科学显式的使用矩阵的例子，不过线性代数世界中，对于一个矩阵它除了可以这样显式表示一组数据之外，还可以表示更加抽象的内容比如一组变换或一个空间,用矩阵表示这些内容是线性代数更加关注的内容.后续见晓.

先尝试构建一个基本的矩阵类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

from .Vector import Vector

class Matrix:
    def __init__(self, list2d):
        self._values = [row[:] for row in list2d]
    
    def col_vector(self, index):
        '''返回矩阵第index个列向量'''
        return Vector([row[index] for row in self._values])
    
    def row_vector(self, index):
        '''返回矩阵第index个行向量'''
        return Vector(self._values[index])
    
    def __getitem__(self, pos):
        '''返回矩阵pos位置的元素'''
        r, c = pos
        return self._values[r][c]

    def size(self):
        '''返回矩阵元素个数'''
        r, c = self.shape()
        return r *c 
    
    def row_num(self):
        '''返回矩阵行数'''
        return  self.shape()[0]
    
    __len__ = row_num
    
    def col_num(self):
        '''返回矩阵列数'''
        return self.shape()[1]
    
    def shape(self):
        '''返回矩阵的形状:(行数, 列数)'''
        return len(self._values), len(self._values[0])

    def __repr__(self):
        return "Matrix({})".format(self._values)
    
    __str__ = __repr__

• 构造函数方式同之前Vector类的构造方式类似，这里假设传入的数据是一个正确的二维数组, 没有设置相应断言.
• 然后就是返回矩阵行数、列数、元素个数、形状、pos位置元素、行向量、列向量等方法，实现比较简单.

矩阵的基本运算和基本性质

同学习向量的套路一样，定义完什么是矩阵之后就开始学习矩阵的基本运算. 前面对于向量的基本运算定义了两种，一种是向量的加法，另一种是向量的数量乘法. 矩阵同样可以对应的定义两种运算，分别是矩阵的加法和矩阵的数量乘法.

矩阵的加法：
$$
A=\begin{pmatrix}a_{11} & a_{12} & … &a_{1c} \
a_{21} & a_{22} & … &a_{2c} \
… & … & … &… \
a_{r1} & a_{r2} & … &a_{rc} \
\end{pmatrix} \quad

B=\begin{pmatrix}b_{11} & b_{12} & … &b_{1c} \
b_{21} & b_{22} & … &b_{2c} \
… & … & … &… \
b_{r1} & b_{r2} & … &b_{rc} \
\end{pmatrix} \
A+B=\begin{pmatrix}a_{11}+b_{11} & a_{12}+ b_{12} & … &a_{1c}+b_{1c} \
a_{21}+b_{21} & a_{22}+b_{22} & … &a_{2c}+b_{2c} \
… & … & … &… \
a_{r1}+b_{r1} & a_{r2}+b_{r2} & … &a_{rc}+b_{rc} \
\end{pmatrix} \
$$
矩阵的数量乘法：
$$
A=\begin{pmatrix}a_{11} & a_{12} & … &a_{1c} \
a_{21} & a_{22} & … &a_{2c} \
… & … & … &… \
a_{r1} & a_{r2} & … &a_{rc} \
\end{pmatrix} \quad
\
k.A=\begin{pmatrix}k.a_{11} & k.a_{12} & … &k.a_{1c} \
k.a_{21} & k.a_{22} & … &k.a_{2c} \
… & … & … &… \
k.a_{r1} & k.a_{r2} & … &k.a_{rc} \
\end{pmatrix} \quad
$$
矩阵的基本运算性质：

• 交换律：$A+B=B+A$
• 结合律：$(A+B)+C=A+(B+C)$
• 存在矩阵$O$ , 满足：$A+O=A$
• 存在矩阵$-A$ ，满足：$A+(-A)=O$
• $-A$ 唯一：$-A=-1.A$
• 数乘结合律：$(ck)A=c(kA)$
• 分配律：$k.(A+B)=k.A+k.B$ ；$(c+k).A=c.A+k.A$

编程实现这些基本运算：(放入Matrix类中)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

@classmethod
def zero(cls, r, c):
    '''返回一个r行c列的零矩阵'''
    return cls([[0]*c for _ in range(r)])

def __add__(self, another):
    '''返回两个矩阵的加法结果'''
    assert self.shape() == another.shape(),\
    "Error in adding. Shape of matrix must be same"
    return Matrix([[a+b for a,b in zip(self.row_vector(i), another.row_vector(i))]
                   for i in range(self.row_num())])

def __sub__(self, another):
    '''返回两个矩阵的减法结果'''
    assert self.shape() == another.shape(),\
    "Error in subtracting. Shape of matrix must be same"
    return Matrix([[a-b for a,b in zip(self.row_vector(i), another.row_vector(i))]
                   for i in range(self.row_num())])

def __mul__(self, k):
    '''返回矩阵的数量乘结果: self * k'''
    return Matrix([[e*k for e in self.row_vector(i)] for i in range(self.row_num())])

def __rmul__(self, k):
    '''返回矩阵的数量乘结果: k*self'''
    return self*k

def __trueidv__(self, k):
    '''返回矩阵的数量除法: self/k'''
    return (1/k)*self

def __pos__(self):
    '''返回矩阵取正的结果'''
    return 1*self

def __neg__(self):
    '''返回矩阵取负的结果'''
    return -1 * self

这些实现过程与Vector类的实现相似.

看待矩阵的另一个视角：系统

在了解了矩阵的基本运算之后，接下来要看矩阵的乘法. 一个矩阵和一个数字相乘是简单的，但是一个矩阵和一个更加复杂的对象相乘可能相对来说更加复杂一些, 先来看看一个矩阵和一个向量的乘法是如何定义的.

看待矩阵最为简单的一个例子就是将其看做数据表格：
$$
语文\quad数学\quad 英语\
A=\begin {pmatrix}
86 & 82 & 92 \
73 & 97 & 84 \
92 & 72 &93 \
\end {pmatrix}
\begin{array}{c}
Dong \
Liu \
Wang
\end{array}
$$
矩阵还可以表示一个系统：

• 经济系统中，对IT、电子、矿产、房产的投入分别为$x_{it}、x_{e}、x_{m}、x_{h}$

$$
\begin{cases}
x_{it}=100+0.2x_e+0.1x_m+0.5x_h \
x_{e}=50+0.5x_{it}+0.2x_m+0.1x_h \
x_{m}=20+0.4x_{e}+0.3x_h \
x_{h}=666+0.2x_{it}
\end{cases}\ \rightarrow

\begin{cases}
x_{it}-0.2x_e-0.1x_m-0.5x_h=100 \
-0.5x_{it}-x_{e}+0.2x_m+0.1x_h =50\
-0.4x_{e}+x_{m}-0.3x_h=20 \
-0.2x_{it}+x_{h}=666
\end{cases}\
$$

假设经济系统投入满足上左式中的关系，这个右边方程组就表达了经济系统.

• 网络(交通网络、信息网络)

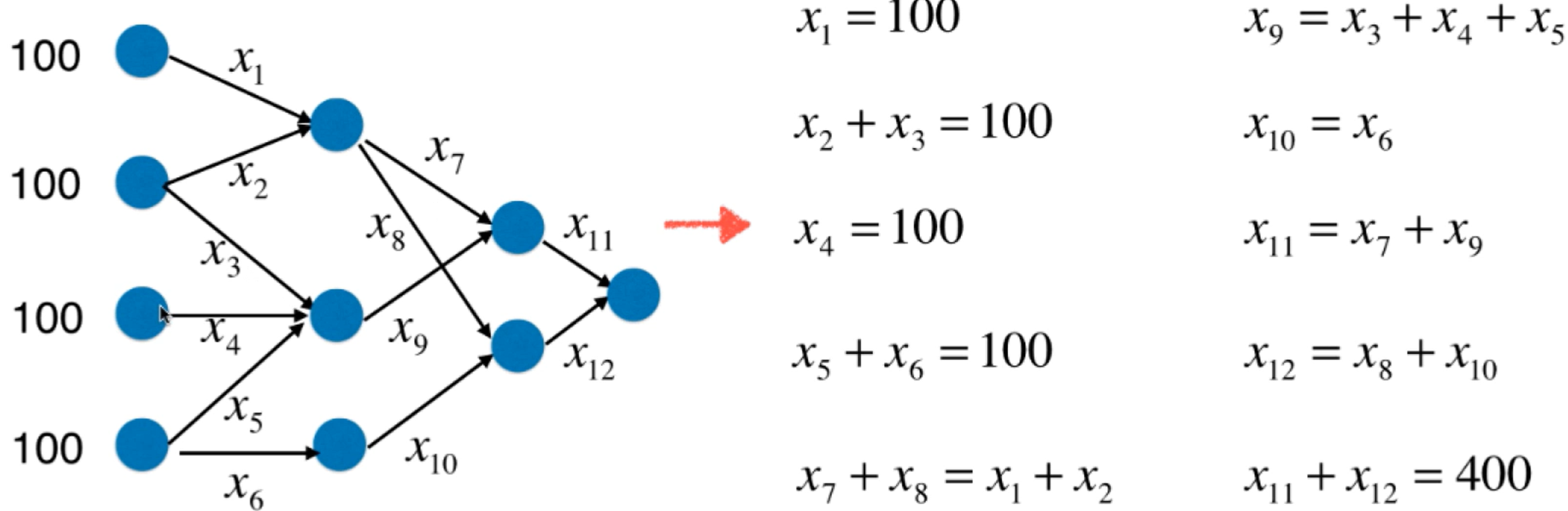
用方程组描述一个网络的流量.

• 电路系统

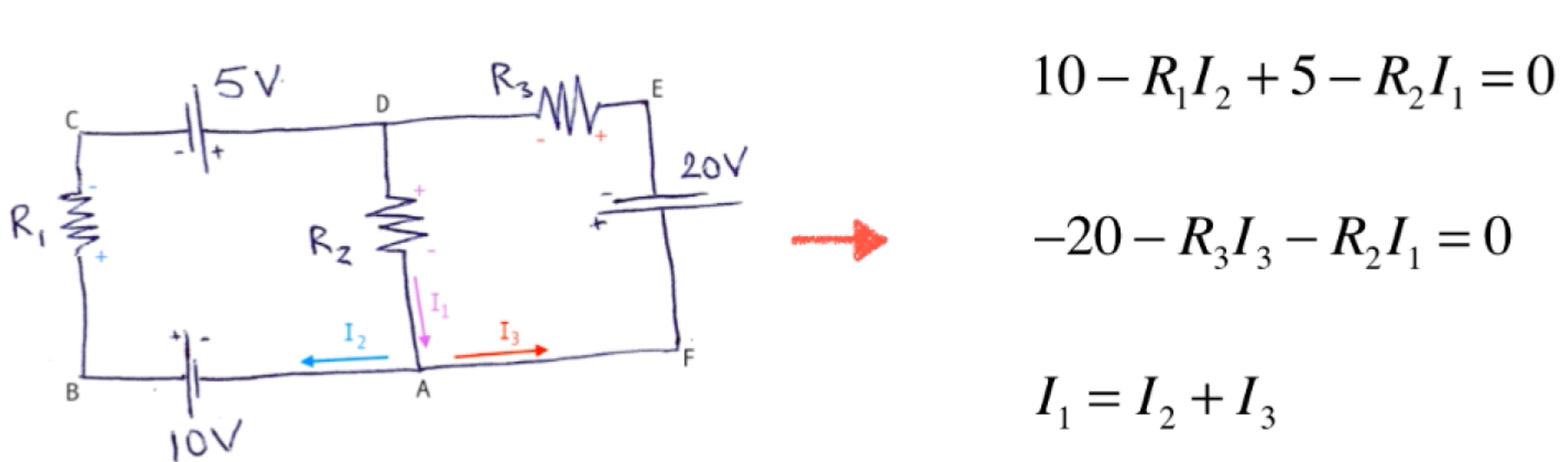
用方程组描述一个电路系统.

线性方程组在各个领域都有着重要的应用，在线性代数中称为线性系统.上面的方程组完全可以用矩阵来表示，因此矩阵就可以表示一个线性系统.

矩阵和向量的乘法

将上面经济系统的例子写成下面的矩阵：
$$
\begin {pmatrix}
1 & -0.2 & -0.1&-0.5 \
-0,5 & -1& 0.2& 0.1 \
0&-0.4 & 1 &-0.3 \
-0.2&0& 0 &1 \
\end {pmatrix}
\begin {pmatrix}
x_{it} \ x_{e} \ x_m\ x_h \
\end {pmatrix}

\begin {pmatrix}
100 \ 50 \ 20\666 \
\end {pmatrix}
$$
用符号表示：
$$
A.\vec{x}=\vec{b}
$$
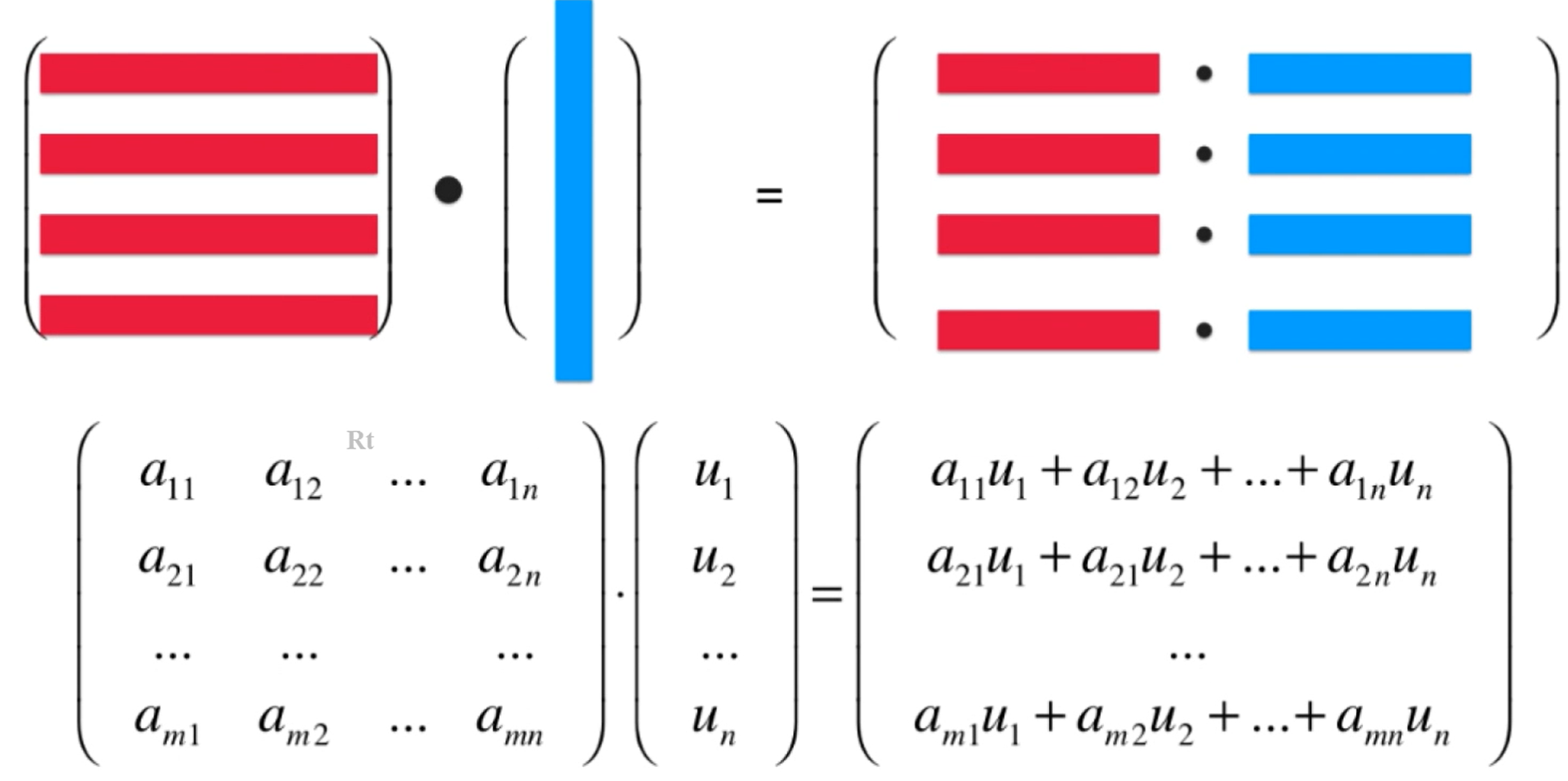
这个运算过程如下图所示，矩阵A有若干行，乘以一个向量，这个向量只有一列，得到的结果也是一个向量，这个结果是把矩阵的每一行拿出来与列向量点乘.

其中矩阵A的列数必须和向量u的元素个数一致，矩阵A的行数没有限制.

如果把矩阵记为T，相乘的列向量记为$\vec{a}$ ,得到的结果就是$\vec{b}$:
$$
T.\vec{a}=\vec{b}
$$
这个过程相当于通过某种方式把向量a转化映射为向量b，这个转化或映射的方式由矩阵T来决定，因此这个矩阵T可以理解为向量的函数.

矩阵和矩阵的乘法

假设一个二维平面，每一个点坐标用一个列向量表示$(x,y)^T$, 如果我想要将每个点的横坐标扩大1.5倍，纵坐标扩大2倍，相应的我们需要通过一种转换使得其变为$(1.5x,2y)^T$ .

矩阵本身可以作为向量的函数，因此上面的问题相当于我们要是找到一个函数，传入$(x,y)^T$ ，得到$(1.5x,2y)^T$ .所以本质需要找到一个变换矩阵T满足下式：
$$
T\begin {pmatrix}
x \ y
\end {pmatrix} =
\begin {pmatrix}
1.5x \ 2y
\end {pmatrix} \
\begin {pmatrix}
a &b \ c&d
\end {pmatrix}
.\begin {pmatrix}
x \ y
\end {pmatrix} =
\begin {pmatrix}
1.5x \ 2y
\end {pmatrix} \
T=\begin {pmatrix}
1.5 &0 \ 0&2
\end {pmatrix}
$$
显然很容易的求解出T.

那么再思考一个问题，如果需要对很多点进行变换，单单每一个点跟这个矩阵T进行乘法操作是可以的，有没有更简单的更批量化的做法呢？这个思路也很简单，只需要把所有的点坐标集合在一起集合成一个矩阵就好了.

以$(0,0),(4,0),(5,3)$ 这三个点为例集合成一起得到：
$$
P=\begin {pmatrix}
0 & 4 & 5\
0 & 0 & 3
\end{pmatrix} \
T.P=\begin {pmatrix}
1.5& 0 \
0 & 2
\end{pmatrix}.\begin {pmatrix}
0 & 4 & 5\
0 & 0 & 3
\end{pmatrix}
\=\begin {pmatrix}
0 & 6 & 7.5\
0 & 0 & 6
\end{pmatrix}
$$
其中P每一列代表一个点坐标.

基于上面的例子其实就得到了矩阵和矩阵的乘法形式：

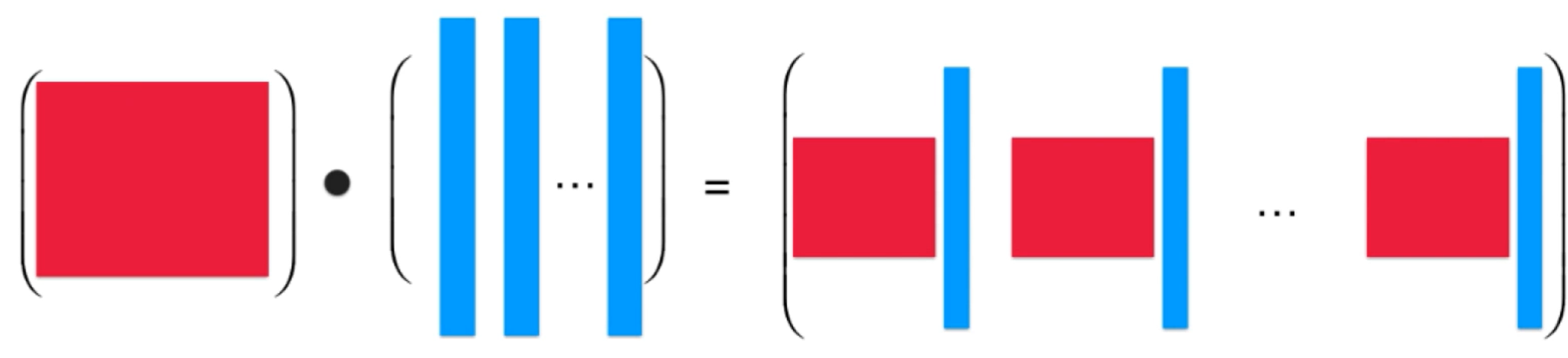
矩阵A与矩阵B相乘可以把矩阵B拆成一个一个的列向量，拆完之后矩阵A分别与矩阵B的每一个列向量进行矩阵和向量的乘法.因此矩阵A的列数必须和矩阵B的行数一致.

• A是m*k的矩阵，B是k*n 的矩阵，则结果是m*n 的矩阵
• 矩阵乘法不遵循交换律，即$A.B\ne B.A$ ，很有可能根本不能相乘.

代码实现矩阵的乘法：(放入Matrix类中)

1
2
3
4
5
6
7
8
9
10
11
12

def dot(self, another):
    '''返回矩阵乘法的结果'''
    if isinstance(another, Vector):
        assert self.col_num() == len(another),\
            "Error in Matrix-Vector Mul"
        return  Vector([self.row_vector(i).dot(another) for i in range(self.row_num())])

    if isinstance(another, Matrix):
        assert self.col_num() == another.row_num(),\
            "Error in Matrix-Matrix Mul"
        return Matrix([[self.row_vector(i).dot(another.col_vector(j)) for j in range(another.col_num())] 
                       for i in range(self.row_num())])

矩阵乘法的性质和矩阵的幂

矩阵乘法不遵守交换律，但矩阵乘法相应也遵循一些性质：

• 结合律：(A.B).C=A.(B.C)
• 分配律：A.(B+C) = A.B + A.C 或（B+C).A=B.A+C.A
• 零矩阵：对任意r*c的矩阵A,存在c*x的矩阵O,满足$A.O_{cx}=O_{rx}$ . 对任意r*c的矩阵A,存在x*r的矩阵O,满足$O_{xr}.A=O_{xc}$ .

了解矩阵的乘法后可以很自然引入矩阵的幂：
$$
A^k=\underbrace{A.A.A…A}_{\text{k}}
$$
显然只有行数和列数相等的矩阵即方阵才可以求出矩阵的幂.跟数字的幂一样，当k>=1时，这个矩阵的幂非常容易求解.但是如果k=0,-1即$A^0,A^{-1},A^{-2}$ 该如何定义呢？后续见晓.

同时需要注意的是$(A+B)^2\ne A^2+2AB+B^2$ ，因为矩阵乘法不满足交换律：
$$
(A+B)^2=(A+B).(A+B)\
=A.A+A.B+B.A+B.B\
=A^2+A.B+B.A+B^2
$$

矩阵的转置

上面的例子中将三个点的坐标写成了列向量的形式：
$$
P=\begin {pmatrix}
0 & 4 & 5\
0 & 0 & 3
\end{pmatrix} \
$$
但实际很多时候我们的数据可能是行向量的形式：
$$
P=\begin {pmatrix}
0& 0 \ 4& 0 \ 5& 3\
\end{pmatrix} \
$$
显然此时的P无法与上面的T矩阵相乘.那么怎么办呢？我们需要对这个矩阵P进行一个转置的操作:
$$
P^T=\begin {pmatrix}
0 & 4 & 5\
0 & 0 & 3
\end{pmatrix} \
$$
矩阵的转置就是将行变成列，列变成行：$A=(a_{ij}),A^T={a_{ji}}$

接着看看矩阵转置的性质：

• $(A^{T})^{T}=A$
• $(A+B)^T=A^T+B^T$
• $(k.A)^T=k.A^T$
• $(A.B)^T=B^T.A^T$

代码实现：(放入Matrix类中)

1
2
3

def T(self):
    '''返回矩阵的转置矩阵'''
    return Matrix([[e for e in self.col_vector(i)] for i in range(self.col_num())])

附完整的Matrix类实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97

from .Vector import Vector

class Matrix:
    def __init__(self, list2d):
        self._values = [row[:] for row in list2d]
    
    @classmethod
    def zero(cls, r, c):
        '''返回一个r行c列的零矩阵'''
        return cls([[0]*c for _ in range(r)])

    def T(self):
        '''返回矩阵的转置矩阵'''
        return Matrix([[e for e in self.col_vector(i)] for i in range(self.col_num())])
    
    def __add__(self, another):
        '''返回两个矩阵的加法结果'''
        assert self.shape() == another.shape(),\
        "Error in adding. Shape of matrix must be same"
        return Matrix([[a+b for a,b in zip(self.row_vector(i), another.row_vector(i))]
                       for i in range(self.row_num())])

    def __sub__(self, another):
        '''返回两个矩阵的减法结果'''
        assert self.shape() == another.shape(),\
        "Error in subtracting. Shape of matrix must be same"
        return Matrix([[a-b for a,b in zip(self.row_vector(i), another.row_vector(i))]
                       for i in range(self.row_num())])
    def dot(self, another):
        '''返回矩阵乘法的结果'''
        if isinstance(another, Vector):
            assert self.col_num() == len(another),\
                "Error in Matrix-Vector Mul"
            return  Vector([self.row_vector(i).dot(another) for i in range(self.row_num())])
        
        if isinstance(another, Matrix):
            assert self.col_num() == another.row_num(),\
                "Error in Matrix-Matrix Mul"
            return Matrix([[self.row_vector(i).dot(another.col_vector(j)) for j in range(another.col_num())] 
                           for i in range(self.row_num())])

    def __mul__(self, k):
        '''返回矩阵的数量乘结果: self * k'''
        return Matrix([[e*k for e in self.row_vector(i)] for i in range(self.row_num())])

    def __rmul__(self, k):
        '''返回矩阵的数量乘结果: k*self'''
        return self*k
    
    def __trueidv__(self, k):
        '''返回矩阵的数量除法: self/k'''
        return (1/k)*self
    
    def __pos__(self):
        '''返回矩阵取正的结果'''
        return 1*self
    
    def __neg__(self):
        '''返回矩阵取负的结果'''
        return -1 * self

    def col_vector(self, index):
        '''返回矩阵第index个列向量'''
        return Vector([row[index] for row in self._values])
    
    def row_vector(self, index):
        '''返回矩阵第index个行向量'''
        return Vector(self._values[index])
    
    def __getitem__(self, pos):
        '''返回矩阵pos位置的元素'''
        r, c = pos
        return self._values[r][c]

    def size(self):
        '''返回矩阵元素个数'''
        r, c = self.shape()
        return r *c 
    
    def row_num(self):
        '''返回矩阵行数'''
        return  self.shape()[0]
    
    __len__ = row_num
    
    def col_num(self):
        '''返回矩阵列数'''
        return self.shape()[1]
    
    def shape(self):
        '''返回矩阵的形状:(行数, 列数)'''
        return len(self._values), len(self._values[0])

    def __repr__(self):
        return "Matrix({})".format(self._values)
    
    __str__ = __repr__