Linear Algebra(6):线性空间（1）

线性代数

Linear Space

线性组合

回忆向量的两个最基本的运算即向量加法和标量乘法：

v + w k v

这两个最基本的运算构成了线性代数中最重要的一个概念线性组合. 对于若干个n维向量 $v_{1} 、 v_{2} \dots v_{p}$ ,则称 $k_{1} . v_{1} + k_{2} . v_{2} + \dots + k_{p} . v_{p}$ 为这些向量的一个线性组合.

我们已经多次见到线性组合了，三维空间中有三个标准单位向量：

e_{1} = (1, 0, 0)^{T} e_{2} = (0, 1, 0)^{T} e_{3} = (0, 0, 1)^{T}

三维空间中的任何一个向量：

v = (x, y, z) = x . (1, 0, 0)^{T} + y . (0, 1, 0)^{T} + z . (0, 0, 1)^{T} = x . e_{1} + y . e_{2} + z . e_{3}

同时以列视角看待矩阵的乘法：

(1425) . (x y) = (x + 2 y 4 x + 5 y) = (14) x + (25) y

矩阵和向量的乘法也是一种列向量的线性组合.

同时Gauss消元法以及Gauss-Jordan消元法整个过程消元之后的结果矩阵每一行对应的是原来矩阵相应行向量的线性组合：

- 1 1 - 3 2 - 4 5 3 - 13 4 000 \to 100 - 2 - 2 - 1 - 3 - 10 - 5 000 \to 100 - 2 10 - 3 50 000 \to 100010750000 r_{1} r_{2} r_{3} \to - r_{1} r_{2} r_{3} \to - r_{1} r_{2} + r_{1} r_{3} - 3 r_{1} \to - r_{1} - \frac{1}{2} (r_{2} + r_{1}) r_{3} - 3 r_{1} \to - r_{1} - \frac{1}{2} (r_{2} + r_{1}) r_{3} - 3 r_{1} - \frac{1}{2} (r_{2} + r_{1}) \to - r_{1} + 2 r_{2} - \frac{1}{2} (r_{2} + r_{1}) r_{3} - 3 r_{1} - \frac{1}{2} (r_{2} + r_{1})

可见最终Gauss-Jordan消元法的结果的每一行是原来矩阵各行的一个线性组合.

线性相关和线性无关

上面经过Gauss-Jordan消元后得到的第三行为零向量：

r_{3} = r_{3} - \frac{7}{2} r_{1} - \frac{1}{2} r_{2} = (0, 0, 0) = O - \frac{7}{2} r_{1} - \frac{1}{2} r_{2} + r_{3} = O

对于这个线性组合有：

k_{1} = - \frac{7}{2} k_{2} = - \frac{1}{2} k_{3} = 1

这三个系数放在三个向量前面使得其结果为零向量，而零向量是我们非常感兴趣的特殊向量，那么还有怎么样的 $k_{1} 、 k_{2} 、 k_{3}$ 使得最终线性组合结果为0?这个问题有个通解就是 $k_{1} = k_{2} = k_{3} = 0$ , 这个问题就引出了线性相关的定义.

对于若干个n维向量 $v_{1}, v_{2}, v_{3}, \dots, v_{p}$ 存在一组k不全为0,使得 $k_{1} . v_{1} + k_{2} . v_{2} + k_{3} . v_{3} + \dots + k_{p} . v_{p} = 0$ 则称 $v_{1}, v_{2}, v_{3}, \dots, v_{p}$ 线性相关.

可线性相关说明这些向量之间不是独立的，可以发现：

r_{3} = \frac{7}{2} r_{1} + \frac{1}{2} r_{2}

即 $r_{3}$ 可以表示成 $r_{1}$ 和 $r_{2}$ 的线性组合. 由此可以得到下面一组等价命题：

如果 v_{1}, v_{2}, v_{3}, ..., v_{p} 线性相关 ⟺ 其中一个向量可以写成其他向量的线性组合

同理容易写出线性无关的定义，对于若干个n维向量 $v_{1}, v_{2}, v_{3}, \dots, v_{p}$ 只有k全部为0时,使得 $k_{1} . v_{1} + k_{2} . v_{2} + k_{3} . v_{3} + \dots + k_{p} . v_{p} = 0$ 则称 $v_{1}, v_{2}, v_{3}, \dots, v_{p}$ 线性无关. 线性无关意味着任何一个向量都不可以表示成其他向量的线性组合.

从向量表达的信息角度看，线性相关意味着这组向量信息是冗余的，其中至少一个向量可以写成其他向量的线性组合，那么这个向量本身并没有表达新的信息；反之线性无关意味着信息的完全不冗余，每一个向量都是独立的，其中一个向量是不能表达成线性组合的形式的。

首先可以得到两个推论：

如果 $v_{1}, v_{2}, v_{3}, \dots, v_{n}$ 线性相关, 则 $v_{1}, v_{2}, v_{3}, \dots, v_{n}, v_{n + 1}$ 线性相关.
如果 $v_{1}, v_{2}, v_{3}, \dots, v_{n}$ 存在零向量, 则 $v_{1}, v_{2}, v_{3}, \dots, v_{p}$ 线性相关.

矩阵的逆和线性相关

线性相关的一个重要性质：m个n维向量 $v_{1}, v_{2}, v_{3}, \dots, v_{m}$ ,若m>n，则 $v_{1}, v_{2}, v_{3}, \dots, v_{m}$ 线性相关.

比如100个三维向量一定线性相关,4个三维向量也一定线性相关,但是3个3维向量就不一定了.先从一个具体的例子出发：

u = (- 3 1) v = (1 - \frac{1}{3}) 是否线性相关？ 是否存在 k_{1}, k_{2} 不全为 0 ，满足 : k_{1} . u + k_{2} v = k_{1} . (- 3 1) + k_{2} . (1 - \frac{1}{3}) = 0 ↓

(- 3 1 1 - \frac{1}{3}) . (k_{1} k_{2}) = 0

可以发现问题转换为了一个线性系统的问题(齐次方程组的问题)，此时可以看这个线性系统是否只有唯一的零解？

很容易化为行最简形式：

(10 - \frac{1}{3} 0) .

一个方程，两个未知数，存在自由列，说明方程组不只有一个解即不只有零解，因此u和v线性相关.

可以发现判断一组向量是否线性相关可以转化成为一个齐次线性方程组的求解问题.

证明一下上面的性质：

P ro f . m 个 n 维向量 v_{1}, v_{2}, v_{3}, ..., v_{m}, 若 m > n ，则 v_{1}, v_{2}, v_{3}, ..., v_{m} 线性相关 . 是否存在 k_{1}, k_{2}, ... k_{m} 不全为 0 ，满足 : k_{1} . v_{1} + k_{2} v_{2} + ... + k_{m} v_{m} = 0 v_{11} v_{12} ... v_{1 n} v_{12} v_{22} ... v_{1 n} ... ... ... ... v_{m 1} v_{m 2} ... v_{mn} . k_{1} k_{2} ... k_{m} = 0 是否有唯一零解？

因为m>n,所以系数矩阵化为行最简形式，肯定非零行小于列数.因此齐次线性方程组肯定有无数解，而不仅仅有唯一的零解.

那么m个n维向量 $v_{1}, v_{2}, v_{3}, \dots, v_{m}$ ,若m>n，何时 $v_{1}, v_{2}, v_{3}, \dots, v_{m}$ 线性无关？显然需要上面的齐次线性方程组有唯一的零解.

上篇提到下面5个等价的命题：

线性系统Ax=0 只有唯一解x=0
矩阵A可逆，A是非奇异矩阵
rref(A)=I
A可以表示成一系列初等矩阵的乘积
Ax=b只有唯一解

因此可以说矩阵A可逆 $⟺$ $v_{1}, v_{2}, v_{3}, \dots, v_{n}$ 线性无关.（可逆则m=n）

到这里对一个方阵A就有下面6个等价命题了：、

方阵A的列向量线性无关
线性系统Ax=0 只有唯一解x=0
矩阵A可逆，A是非奇异矩阵
rref(A)=I
A可以表示成一系列初等矩阵的乘积
Ax=b只有唯一解

生成空间

如下图所示，二维空间中的任何向量都可以表示为u和v的线性组合，可以说u和v生成了整个二维空间.

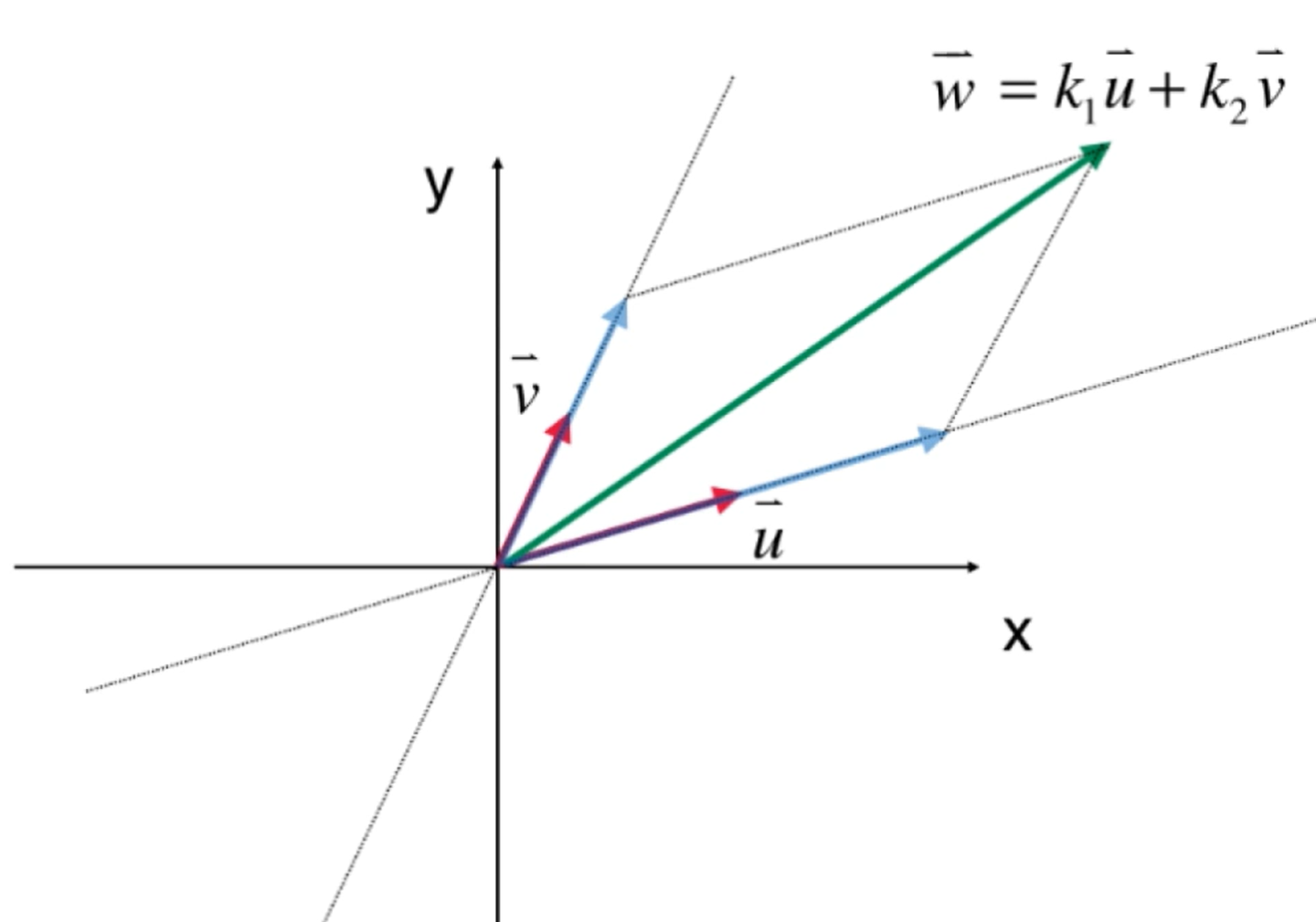
把这个结论推而广之，若空间中的所有向量都可以表示为 $v_{1}, v_{2}, v_{3}, \dots, v_{p}$ 的线性组合，则称这些向量可以生成这个空间.

但是上面图中的二维空间中 $u, v, w$ 也可以生成整个二维空间, 那么最少需要几个向量生成二维空间？显然对于一个n维空间，至少需要n个向量才能够生成.

接下来的问题就是n个向量一定可以生成n维空间吗？显然不是，如果上图中的u和v共线就不能生成n维空间.那么n个向量何时可以生成n维空间？

上述问题依然可以写成下面的线性系统，如果要有解，其系数矩阵必须可以化为行最简形式，并且此时是唯一解.

v_{11} v_{12} ... v_{1 n} v_{12} v_{22} ... v_{2 n} ... ... ... ... v_{n 1} v_{n 2} ... v_{nn} u_{1} u_{2} .. u_{n} \to 10 ... 0 01 ... 0 ... ... ... ... 00 ... 1 u_{1} u_{2} ... u_{n}

到这里对一个方阵A就有下面7个等价命题了：

方阵A的列向量可以生成n维空间
方阵A的列向量线性无关
线性系统Ax=0 只有唯一解x=0
矩阵A可逆，A是非奇异矩阵
rref(A)=I
A可以表示成一系列初等矩阵的乘积
Ax=b只有唯一解

空间的基

对于一组向量来说，如果空间中所有的向量都可以用表示成这组向量的线性组合，那么可以说这组向量生成了整个空间. 若m个向量生成n维空间，m最小为n；m个n维向量 $v_{1}, v_{2}, v_{3}, \dots, v_{m}$ ,若m>n，则 $v_{1}, v_{2}, v_{3}, \dots, v_{m}$ 线性相关. 因此若m个n维向量线性无关，m最大为n.

那么若一组向量既可以生成整个n维空间，且线性无关，这组向量一定有n个，则称这组向量为这个n维空间的一组基.

n个n维向量 $v_{1}, v_{2}, v_{3}, \dots, v_{n}$ ,若他们是这个n维空间的基，等价于：

$v_{1}, v_{2}, v_{3}, \dots, v_{n}$ 生成整个n维空间
$v_{1}, v_{2}, v_{3}, \dots, v_{n}$ 线性无关

一个空间有无数组基，以二维空间为例，只要两个向量u和v不共线，这两个向量就是这个而空间的基.

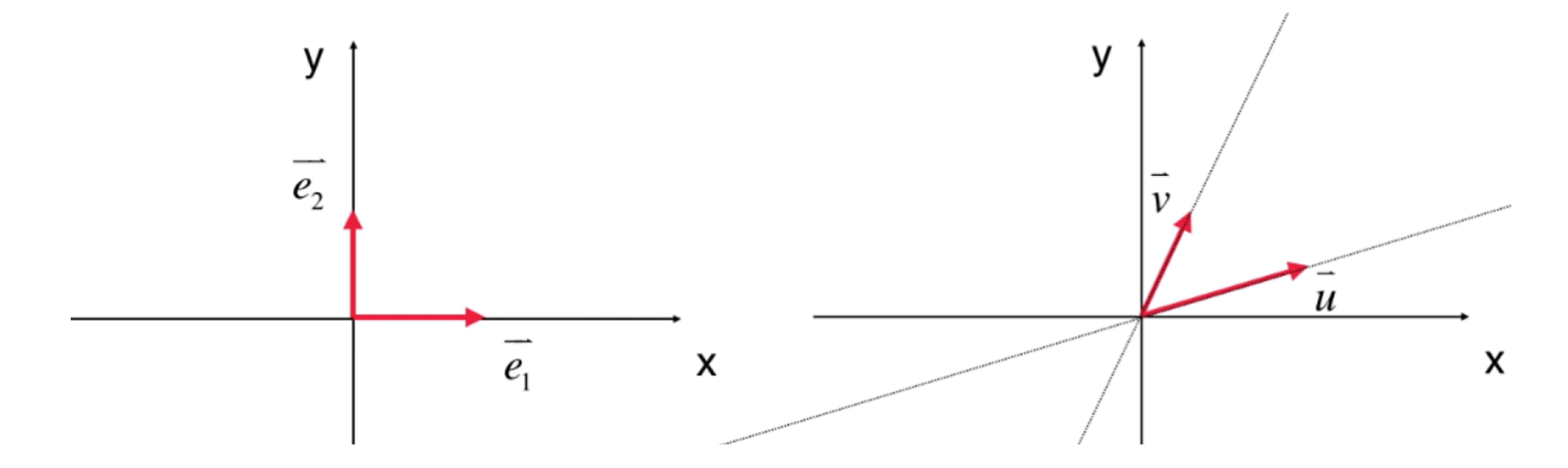
如上图所示，这两组向量都是二维空间的基.我们最常用的是左边的标准正交基.

可以得到空间的基的一些性质如下：

n维空间中，任意n个线性无关的向量，一定是这个n维空间的基.

n维空间中，如果n个向量可以生成整个空间，则这n个向量是这个n维空间的基.

如果n维空间中的p个向量 $v_{1}, v_{2}, v_{3}, \dots, v_{p}$ 线性无关，则 $p \leq n$

如果p个向量 $v_{1}, v_{2}, v_{3}, \dots, v_{p}$ 可以生成n维空间，则 $p \geq n$

如果p个向量 $v_{1}, v_{2}, v_{3}, \dots, v_{p}$ 是n维空间的基，则 $p = n$

如果一组向量 $v_{1}, v_{2}, v_{3}, \dots, v_{p}$ 可以生成n维空间，则这组向量的一个子集是n维空间的一组基.