线性代数
Linear Space
空间
空间是一个集合. 线性代数中前面提到的二维空间、三维空间本质也是集合，通常把这些空间称为欧几里得空间.欧几里得空间是有序实数元组的集合，比如（6，66）属于二维欧几里得空间；（3.14，0，sqrt(2)）属于三维欧几里得空间.
其实欧几里得空间就是点集，是起点为原点的向量集合.同时欧几里得空间还被称为向量空间, 空间中的元素是“向量”. 这里注意向量的定义是很广泛的，不仅仅是指前面提到的起点在原点有方向就是一个向量，实际上这是欧几里得空间中的向量，还存在其他的向量空间向量是其他样子的.
那么到底什么是向量？向量首先必须定义两种运算加法运算和数量乘法运算. 并且这两种运算还要满足10条性质：
对于一个向量空间V:
- 如果u,v都属于V,则u+v属于V (封闭性)
- 如果u属于V,k是一个实数，则ku属于V (封闭性)
- 加法交换律：u+v=v+u
- 加法结合律：(u+v)+w=u+(v+w)
- 存在O属于向量空间，使得u+O=u
- 对于每一个u存在-u,使得u+（-u）=O
- 数量乘结合律：（kc）u=k(cu)
- 数量乘分配律：（k+c）u=ku+cu
- 数量乘分配律：k(u+v)=ku +kv
- 1*u=u
因此定义两种运算且满足上述性质才称为“向量”.最常见的欧几里得空间$R^n$ 是向量空间.
广义向量空间
向量空间就是一个集合，集合中的元素可以定义两种运算加法和数量乘法，使得满足10条性质. 我们通常说的向量就是指欧几里得空间中的元素.为了区别，通常把非欧几里得空间的向量空间称为广义向量空间.
比如所有的2*2方阵，构成了一个向量空间. 加法可以采用矩阵加法的定义，数量乘法采用矩阵数量乘法的定义. 显然其满足上面10条性质.
所有的n阶方阵，也可以构成一个向量空间.；所有的2*3的矩阵，构成一个向量空间；所有的m*n矩阵构成了一个向量空间.
上面都是矩阵相关的例子，数学上的一个里就是所有的多项式构成一个向量空间.
$$
a_px^p+a_{p-1}x^{p-1}+…+a_1x+a_0x^0
$$
加法就定义为多项式加法，数量乘法就是多项式乘以一个数.
下面22的方阵左边就能构成一个向量空间，而右边就不行：
$$
\begin{pmatrix}
a & 0\
0 &b
\end{pmatrix} \quad
\begin{pmatrix}
1 & 0\
0 &b
\end{pmatrix}
$$
同时*所有的某类函数也能构成一个向量空间.
但我们最常见常用的还是欧几里得空间$R^n$ ，即由所有的n维有序元组构成的向量空间.
子空间
假设V是一个向量空间，如果S是V的子集，且S还是一个向量空间，则称S是V的一个子空间.
举个例子，所有的2阶方阵形成了一个向量空间V，而所有如下形式的矩阵形成了一个向量空间S:
$$
\begin{pmatrix}
a & 0\
0 &b
\end{pmatrix}
$$
此时S就是V的一个子空间.
而下面形式的矩阵虽然是S的一个子集，但却不是一个向量空间：
$$
\begin{pmatrix}
1 & 0\
0 &b
\end{pmatrix}
$$
此时这个矩阵形成的集合就不是S的一个子空间.
上面定义中比较难判断的就是“且S还是一个向量空间”这个条件，因为要看是否满足那10个性质. 而其实这个条件可以置换成“且S对加法和数量乘法封闭”,即下面的描述：
假设V是一个向量空间，如果S是V的子集，且S对加法和数量乘法封闭，则称S是V的一个子空间.
为什么可以替换呢？条件置换后，10条性质首先会满足下面的8条：
对于一个向量空间V:
- 如果u,v都属于V,则u+v属于V (封闭性)
- 如果u属于V,k是一个实数，则ku属于V (封闭性)
- 加法交换律：u+v=v+u
- 加法结合律：(u+v)+w=u+(v+w)
- 数量乘结合律：（kc）u=k(cu)
- 数量乘分配律：（k+c）u=ku+cu
- 数量乘分配律：k(u+v)=ku +kv
- 1*u=u
其中下面这6条描述的是加法和数量乘法运算的性质，因为V是一个向量空间，那么在V上已经定义了向量加法和数量乘法，这些加法和乘法就肯定满足这些运算性质，而S是V的一个子空间，所以在其上面定义的两种运算是没有变化的，依然满足这6条性质。
剩下了这两条性质：
- 存在O属于向量空间，使得u+O=u
- 对于每一个u存在-u,使得u+（-u）=O
若V是一个向量空间，有0u=O
$$
Prof.\quad 0 =0+0 \
0u=(0+0)u \
0u=0u+0u\
因为向量空间V中的每一个向量u都存在-u使得u+(-u)=O\
因此对于0u也存在-0u使得0u+(-0u)=O\
0u+(-0u)=0u+0u+(-0u)\
O=0u+O\
可得O=0u
$$
若V是一个向量空间，则-u=-1u
$$
u+(-1u)\=1u+(-1)u\
=（1-1)u\
=0u\
=O\ 已知对于每一个u存在-u,使得u+（-u）=O\因此
-1u=-u
$$
而此时对于u属于子空间S也满足剩下这两条性质：
- 存在O属于S，使得u+O=u
- 对于每一个u存在-u属于S,使得u+（-u）=O
因为S对加法和数量乘法封闭，因此0u数量乘法也一定封闭，、0u属于S即零向量一定在S中，同理-1u属于S即-u属于S.上述两条性质满足.
可以发现V的任何一个子空间都一定包含零向量O; 对于V的任何子空间S, 如果u属于S, 则-u一定属于S.
欧几里得空间的子空间
以二维平面为例：
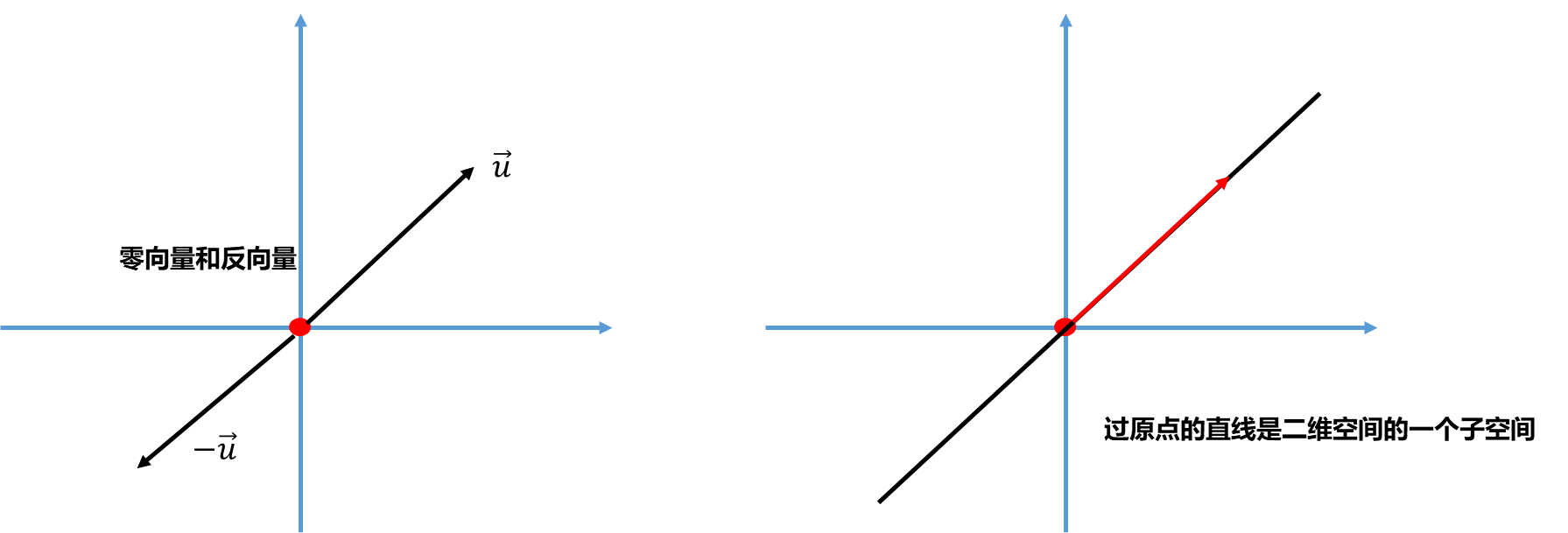
二维平面就是二维欧几里得空间，对于一个向量空间一定存在一个零向量即n维空间的坐标原点(上图中红点处)，以及对于任意个向量u都能找反向量-u. 如上右图所示，在二维平画一条过原点直线，这条直线就是这个二维空间的一个子空间. 这条直线上的所有向量对加法和数量法都是封闭的.
但是所有的直线都是二维欧几里得空间的子空间吗？显然不是，下面就是两个反例：
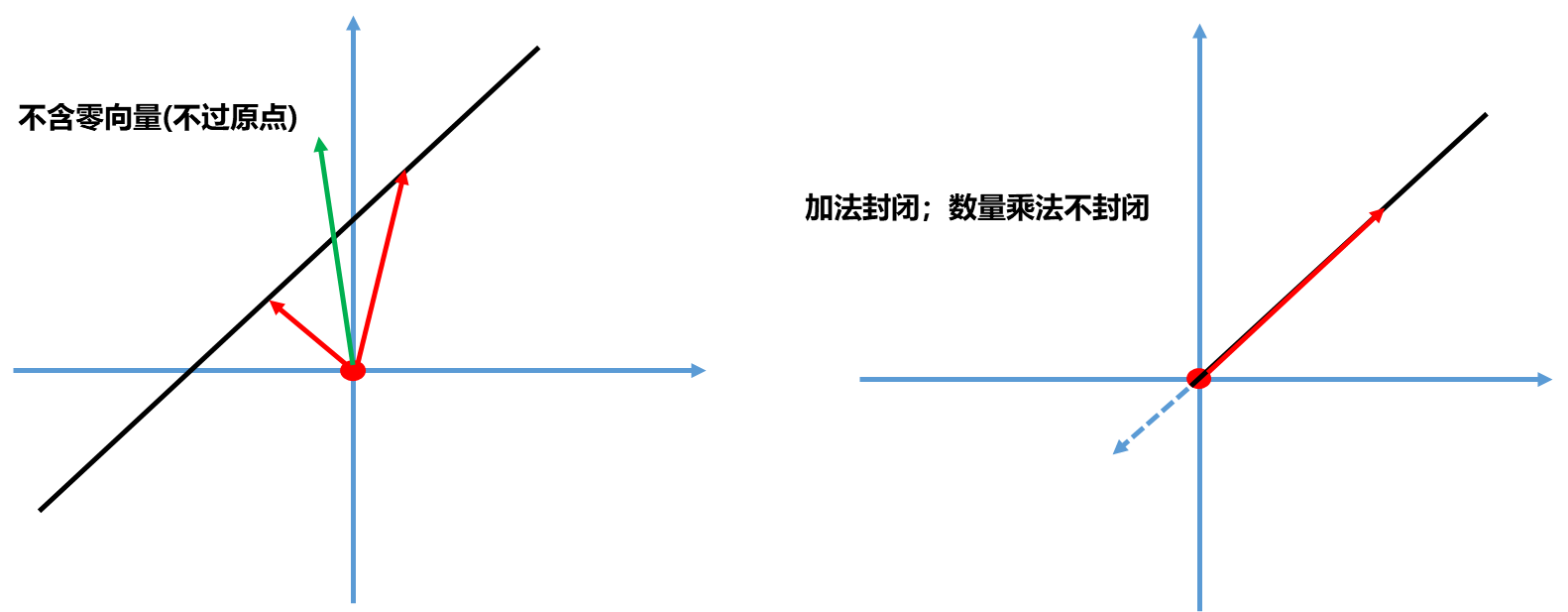
- 左图是一条不过原点的直线，随机取两个向量，其加法得到的向量(绿色)显然不在直线上，加法不封闭.，显然数量乘法也不封闭. 并且不含零向量肯定不是一个子空间.
- 右图是一条过原点的射线，包含零向量，但是显然加法封闭，数量乘法不封闭.
因此二维空间任意一条过原点的直线都是其子空间.
拓展到三维空间：
- 过原点的一个平面，是三维空间的一个子空间
- 过原点的一条直线，是三维空间的一个子空间
- 原点本身，是三维空间的一个子空间
对于n维空间来说，过原点的一个m(m<n)维空间，是n维空间的一个子空间.
维度
n维空间中这个维度是什么？首先前面提到过空间的基是指一组向量满足两个条件：(1)生成空间(2)线性无关.
一个空间的基中，向量的个数，称为维度.
- 二维欧几里得空间的维度为2。$e_1=(1,0)^T,e_2=(0,1)^T$ ，因此$dim(R^2)=2$
- 三维欧几里得空间的维度为3。$e_1=(1,0,0)^T,e_2=(0,1,0)^T,e_3=(0,0,1)^T$ ，因此$dim(R^3)=3$
- n维欧几里得空间的维度为n. $dim(R^n)=n$
一个欧几里得空间的任何一组基，其中的向量个数是相同的. 一个欧几里得空间的维度是固定的.
一个欧几里得空间中的每一个有序实数元组包含n个元素，这个空间维度一定为n吗？显然不对，涉及到子空间概念就不对，像上面例子中二维空间中的一条直线，这条直线上每一个有序实数元组比如(1,1)包含2个元素，但是维度却为1而不是2.
举个例子，被向量u=(2,0,0)；v=(-1，0，0)；w=(0,0,1)生成的空间，维度是多少？显然u和v线性相关，所以可以删除一个比如u，此时v和w线性无关，所以这个生成空间的维度为2.
上面例子也可以得到一个结论：
- 一组n维向量$v_1,…v_p$ 的生成空间，是n维空间的子空间. (上面例子中u,v,w是3维向量，其生成空间是2维的)
行空间和行秩
上面的例子中“被向量u=(2,0,0)；v=(-1，0，0)；w=(0,0,1)生成的空间，维度是多少？”，我们的解决方案是：
- u和v线性相关，所以可以删除u或v
- v和w线性无关，所以这个生成空间的维度为2.
这个问题本质上是给出一组n维向量$v_1,v_2,…v_p$， 其生成空间的维度是多少？这个问题求解过程本质上是找到这组向量有多少和其他向量线性相关.上面是个简单的例子，可以一眼看出来，但如果向量数量更多并且向量维度更大，很显然很难直接判断出来.有没有别的系统性的方法得到这个问题答案？
前面提到过Gauss-Jordan消元法的结果的每一行，是原来矩阵各行的一个线性组合：
$$
\left(
\begin{array}{ccc|c}
-1 & 2 & 3 & 0 \
1 & -4 & -13 & 0\
-3 & 5 & 4 & 0
\end{array}
\right) \rightarrow
\left(
\begin{array}{ccc|c}
1 & -2 & -3 & 0 \
0 & -2 & -10 & 0\
0 & -1 & -5 & 0
\end{array}
\right) \rightarrow
\left(
\begin{array}{ccc|c}
1 & -2 & -3 & 0 \
0 & 1 & 5 & 0\
0 & 0 & 0 & 0
\end{array}
\right) \rightarrow
\left(
\begin{array}{ccc|c}
1 & 0 & 7 & 0 \
0 & 1 & 5 & 0\
0 & 0 & 0 & 0
\end{array}
\right) \
\left(
\begin{array}{c}
\vec{r_1} \
\vec{r_2}\
\vec{r_3}
\end{array}
\right) \rightarrow
\left(
\begin{array}{c}
-\vec{r_1} \
\vec{r_2}\
\vec{r_3}
\end{array}
\right) \rightarrow
\left(
\begin{array}{c}
-\vec{r_1} \
\vec{r_2}+\vec{r_1}\
\vec{r_3}-3\vec{r_1}
\end{array}
\right) \rightarrow
\left(
\begin{array}{c}
-\vec{r_1} \
-\frac{1}{2}(\vec{r_2}+\vec{r_1})\
\vec{r_3}-3\vec{r_1}
\end{array}
\right) \rightarrow
\left(
\begin{array}{c}
-\vec{r_1} \
-\frac{1}{2}(\vec{r_2}+\vec{r_1})\
\vec{r_3}-3\vec{r_1}-\frac{1}{2}(\vec{r_2}+\vec{r_1})
\end{array}
\right) \rightarrow
\left(
\begin{array}{c}
-\vec{r_1} +2\vec{r_2}\
-\frac{1}{2}(\vec{r_2}+\vec{r_1})\
\vec{r_3}-3\vec{r_1}-\frac{1}{2}(\vec{r_2}+\vec{r_1})
\end{array}
\right)
$$
以最终结果的第三行为例：
$$
\vec{r_3}=\frac{7}{2}.\vec{r_1}+\frac{1}{2}.\vec{r_2}
$$
r3可以表示为r1和r2的线性组合，即三个向量线性相关.可以把r3给删除掉. 同理如果Gauss-Jordan消元法一共有m行，假设下面有x行为0,就意味着这x行所对应的行向量都可以表示成上面m-x行向量的线性组合，这x个最终为0向量的向量都可以删去.
因此这个问题的一般化求解方法：
- 将这组向量按照行排列成一个矩阵
- 执行Gauss-Joran消元法化为RREF, 非零行的个数即为其生成空间的维度.
$$
\left(
\begin{array}{}
\vec{u}\
\vec{v}\
\vec{w}\
\end{array}
\right) =
\left(
\begin{array}{}
2 & 0&0 \
-1&0&0\
0&0&1
\end{array}
\right) =
\left(
\begin{array}{}
1 & 0&0 \
-1&0&0\
0&0&1
\end{array}
\right) =
\left(
\begin{array}{}
1 & 0&0 \
0&0&0\
0&0&1
\end{array}
\right) =
\left(
\begin{array}{}
1 & 0&0 \
0&0&1\
0&0&0\
\end{array}
\right) \
$$
对于一个矩阵，行向量生成的空间，称为行空间(Row Space);列向量生成的空间，称为列空间(Column Space).
比如下面3行4列的矩阵：
$$
\begin{pmatrix}
1&2&3&4\
5&6&7&8\
9&10&11&12
\end{pmatrix}
$$
行空间是4维空间的子集，列空间是3维空间的子集. 拓展m行n列，行空间是n维空间的子集，裂空间是m维空间的子集.
一个矩阵的行最简形式的非零行数量称为矩阵的行秩(Row Rank). 行空间的维度为矩阵的行秩. 并且一个矩阵的行最简形式的非零行向量是A的行空间的一组基.
列空间和列秩
依然从上面的那个问题出发，我们以列的视角直接看这三个向量是否线性无关：
$$
k_1\left(
\begin{array}{}
2\
0\
0\
\end{array}
\right)+
k_2\left(
\begin{array}{}
-1\
0\
0\
\end{array}
\right)+
k_3\left(
\begin{array}{}
0\
0\
1\
\end{array}
\right)=
\left(
\begin{array}{}
2&-1&0\
0&0&0\
0&0&1\
\end{array}
\right)\left(
\begin{array}{}
k_1\
k_2\
k_3
\end{array}
\right)=0
$$
现在就是看这个线性方程组是否只有唯一解.现在方程组是一个齐次线性方程组，等号右边全为0，只需要看系数矩阵.
$$
\left(
\begin{array}{}
2&-1&0\
0&0&0\
0&0&1\
\end{array}
\right)=
\left(
\begin{array}{}
1&-0.5&0\
0&0&0\
0&0&1\
\end{array}
\right)=
\left(
\begin{array}{}
1&-0.5&0\
0&0&1\
0&0&0\
\end{array}
\right)
$$
此时的两个1分别对应两个主元列.而-0.5对应的是自由列.
- 自由列上的元素意味着可以随便取值，当然可以取非零值. 因此显然线性相关、
- 自由列的个数，为可以表示为其他向量线性组合的向量个数
- 主元列的个数，为线性无关的向量个数，即维度！
而主元列的个数，为列秩(Column Rank).
对于一个矩阵，列向量生成的空间称为列空间(Column Spcae). m行n列，列空间是m维空间的子空间. 而一个矩阵的行最简形式的主元列数量称为矩阵的列秩. 列空间的维度为矩阵的列秩.
行最简形式主元列的对应的原矩阵的列，是列空间的一组基. 注意和行空间的区别，行最简形式中的非零行，不是一组基.
矩阵的秩和矩阵的逆
对于一个给定的矩阵，它的行秩和列秩总是相等的，这个共同的值就称为矩阵的秩。 也说明了一个矩阵的行空间和列空间维度相等.
$$
矩阵的秩=矩阵的行秩=矩阵的列秩
$$
比如判断u=(1，1，2)，v=(2，2，3)，w=(3,3,4)的生成空间的维度？
$$
\left(
\begin{array}{}
1&1&2\
2&2&3\
3&3&4\
\end{array}
\right)
$$
从行角度很难看这三个向量是否线性相关，但是从列的角度一眼看出第一列和第二列相等，这个矩阵列秩最大为2，因此行秩也最大为2.
对于一个m行n列的矩阵，行空间是n维空间的子空间，列空间是m维空间的子空间.
对于一个n阶方阵，行空间是n维空间的子空间，列空间是n维空间的子空间. 那么何时行空间和列空间都是n维空间？即矩阵的秩r=n.此时也称n阶方阵是满秩(full rank).
满秩情况下行最简形式的非零行个数为n,主元列个数为n.此时行最简形式就是一个单位矩阵,
到这里对于一个方阵A的等价命题可以在进行拓展：
到这里对一个方阵A就有下面13个等价命题了：
方阵A的列向量可以生成n维空间
方阵A的列向量线性无关
线性系统Ax=0 只有唯一解x=0
矩阵A可逆 ，A是非奇异矩阵
rref(A)=I
A可以表示成一系列初等矩阵的乘积
Ax=b只有唯一解
方阵A的列向量是n维空间的基
A为满秩矩阵(秩=n)
A的行秩为n
A的列秩为n
A的行空间为$R^n$
A的列空间为$R^n$
代码实现矩阵的秩：
1 | def rank(A): |
零空间
一个齐次线性方程组的所有解，形成一个向量空间. 如何证明呢？首先一个齐次线性方程组一定有解，要么零解或者无数解.只有零解时是一个向量空间，而无数解时如何证明？只需证明对向量加法和数量乘法封闭.
如果系数矩阵为m*n的矩阵，解为n维向量.如果解形成向量空间，则该向量空间是n维空间的一个子空间.
假设系数矩阵为A, 假设u和v都是解，则有：
$$
A.\vec{u}=O\
A.\vec{v}=O\
A.\vec{u}+A.\vec{v}=O \
A.(\vec{u}+\vec{v})=O
$$
说明u+v也是齐次线性方程组的解.满足加法封闭.
假设u是解
$$
A.\vec{u}=O\
k.A.\vec{u}=O\
A.(k\vec{u})=O\
$$
说明ku也是方程组的解.满足数量乘法封闭.
因此一个齐次线性方程组的所有解形成一个向量空间，称这个空间为零空间(Null Space).
把矩阵看作系统，这个视角下, A的零空间，就是$Ax=0$ 中，所有x组成的空间. 矩阵可以看做向量的函数，在这个视角下，零空间是一个集合，集合中的所有的向量，在A的变换下，都将映射到零点. 矩阵同时可以看做空间，在这个视角下，此时零空间是一个集合，这个集合中的所有的向量，和A的行向量点乘结果为0.
而点乘结果为0，意味着这个集合中的所有向量，和A的行空间中所有向量垂直(正交).即A的行空间和A的零空间正交.
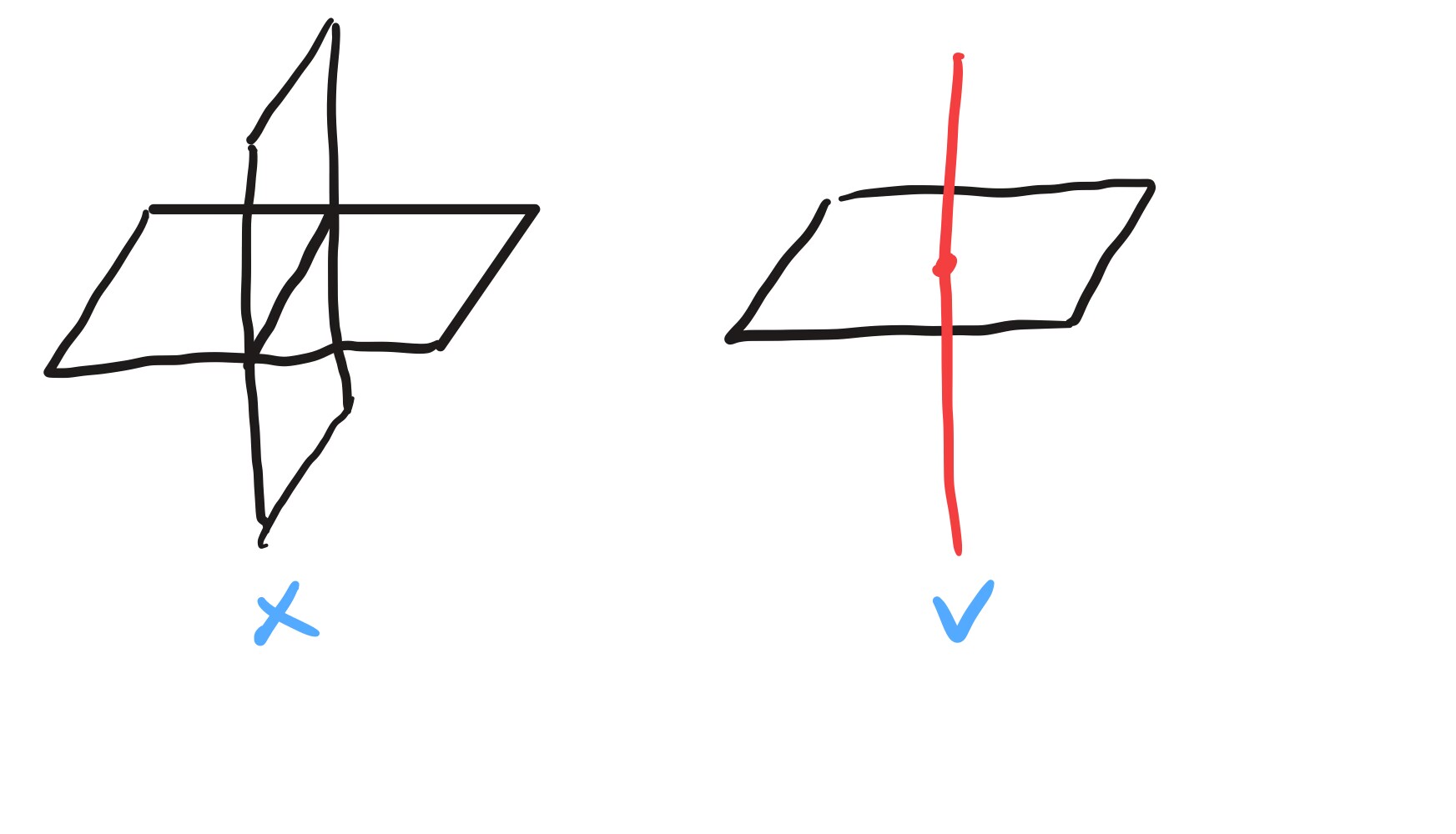
- 上图中左边是两个二维平面，这两个平面是垂直的，但是将这两个平面看做两个空间，这两个空间不正交. 比如两个平面相交的线上的向量同时属于两个平面，不正交.
- 但是右边这个一条直线垂直一个平面看做两个子空间，直线上的任何一个向量和平面上的任何一个向量都垂直，这两个空间是正交的.
这两个二维平面在三维空间中是不可能正交的，但是在四维空间是可以正交的，但是无法直观绘制出来,很抽象.
零空间的基和秩-零化度定理
对于一个矩阵A来说，$Ax=0$ 所有的解x构成的空间叫做零空间. 那么零空间的维度是多少？能否给出一组基？由于零空间是齐次线性方程组所有的解构成的空间，因此需要从解齐次线性方程组开始：
$$
\left(
\begin{array}{}
-1&1&2\
1&-4&-13\
-3&5&4\
\end{array}
\right) \rightarrow
\left(
\begin{array}{}
1&0&7\
0&1&5\
0&0&0
\end{array}
\right) \rightarrow
\begin{cases}
x_1+7x_3=0\
x_2+5x_3=0\
x_3
\end{cases}
$$
$$
\left(
\begin{array}{}
x_1\
x_2\
x_3
\end{array}
\right)=
\left(
\begin{array}{}
-7x_3\
-5x_3\
x_3
\end{array}
\right)=\left(
\begin{array}{}
-7\
-5\
1
\end{array}
\right)x_3
$$
可以发现这个例子矩阵A零空间的维度为1，其一组基为$(-7,-5,1)^T$ .
看一个更复杂的例子：
$$
\left(
\begin{array}{}
1&2&3&4&5&6\
27&28&29&30&31&32\
15&16&17&18&19&20\
31&32&33&34&35&36\
45&46&47&48&49&50\
\end{array}
\right) \rightarrow
\left(
\begin{array}{}
1&0&-1&-2&-3&-4\
0&1&2&3&4&5\
0&0&0&0&0&0\
0&0&0&0&0&0\
0&0&0&0&0&0\
\end{array}
\right)\
=\left(
\begin{array}{}
1\
-2\
1\
0\
0\
0
\end{array}
\right)x_3+
\left(
\begin{array}{}
2\
-3\
0\
1\
0\
0
\end{array}
\right)x_4+
\left(
\begin{array}{}
3\
-4\
0\
0\
1\
0
\end{array}
\right)x_5+
\left(
\begin{array}{}
4\
-5\
0\
0\
0\
1
\end{array}
\right)x_6
$$
可以发现主元列有2个，自由列有4个. 这个齐次线性方程组的解拆成了四个向量的和，这其实就是这四个向量的生成空间. 即这个齐次线性方程组的解就是这个生成空间，这个生成空间也就是这个矩阵的零空间. 显然这个零空间的维度为4，这也是零空间的一组基.
到这里就回答了如何求一个矩阵A零空间的维度以及零空间的基. 零空间的维度就看自由列有多少列，而零空间的基本质是求出解空间，对解空间进行简单的变形后就能看出是一个像上面例子的若干列的线性组合, 这些列就是零空间的基.
对于一个m*n的矩阵，将其化为行最简形式，主元列数为列空间的维度，自由列数为零空间的维度. 而列空间的维度+零空间的维度=n.
而列空间的维度就是矩阵的秩(rank)，零空间的维度叫做零化度(Nullity)：
$$
rank+nullity=n
$$
这就是秩-零化度定理.
对比一下列空间和零空间：
(1) 对于一个m行n列的矩阵，列空间：Ax=v（x任取），列空间是m维空间的子空间，列空间的维度为行最简形式中主元列数。主元列的对应原矩阵的列是列空间的一组基.
(2)零空间：Av=0, 零空间是n维空间的子空间，零空间的维度是行最简形式中自由列数.
何时零空间维度为0?显然当列空间维度为n时，对于方阵即为满秩的时候.
到这里对一个方阵A就有下面14个等价命题了：
方阵A的列向量可以生成n维空间
方阵A的列向量线性无关
线性系统Ax=0 只有唯一解x=0
矩阵A可逆 ，A是非奇异矩阵
rref(A)=I
A可以表示成一系列初等矩阵的乘积
Ax=b只有唯一解
方阵A的列向量是n维空间的基
A为满秩矩阵(秩=n)
A的行秩为n
A的列秩为n
A的行空间为$R^n$
A的列空间为$R^n$
A的零空间为{O}.
左零空间和四大子空间
四大子空间的联系和区别：
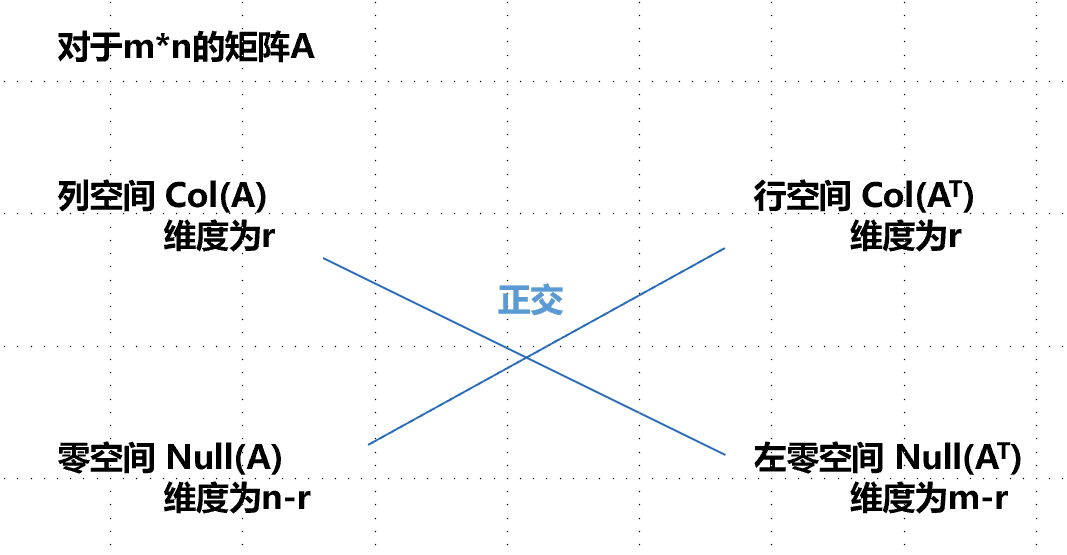
为什么$Null(A^T)$ 叫做A的左零空间:
$$
A^Tx=0\
(A^Tx)^T=0\
x^TA=0
$$
零空间是Ax=0所有x组成的空间，而上面是$x^TA=0$ 即左乘，因此叫做左零空间.
为什么要研究子空间？
研究子空间是因为全空间（如 $\mathbb{R}^n$）往往太大、太杂乱，而无论是自然界的数据还是方程组的解，通常只“栖息”在一个更小的、有特定结构的角落里。
- 子空间的维度大大降低
- 其他一些应用的基础，很多问题就是Ax=b, 寻找A的列空间中离b最近的b’，Ax=b’