Linear Algebra(9):坐标转换和线性变换

线性代数

坐标转换和线性变换

空间的基和坐标系

前面讨论了什么是空间，什么是向量空间，什么是子空间，对于一个空间来说基是一个非常重要的属性并且一个空间是有无数组基的，那么一个空间的一组基和另外一组基是怎么变换的？

理解空间的基的一个视角就是坐标系，坐标系和空间的基是一一对应的关系，有了空间的基就可以说有了空间的坐标系,有了空间的坐标系就可以说有了空间的基.

举个例子，如下左图二维平面坐标系取一点(12,8),这个坐标是建立在图中红色箭头即一组基的基础上. 同时二维平面有无数组基，因此右图中的一组基又定义了一个坐标系，此时红点的坐标就变成了(2,2).

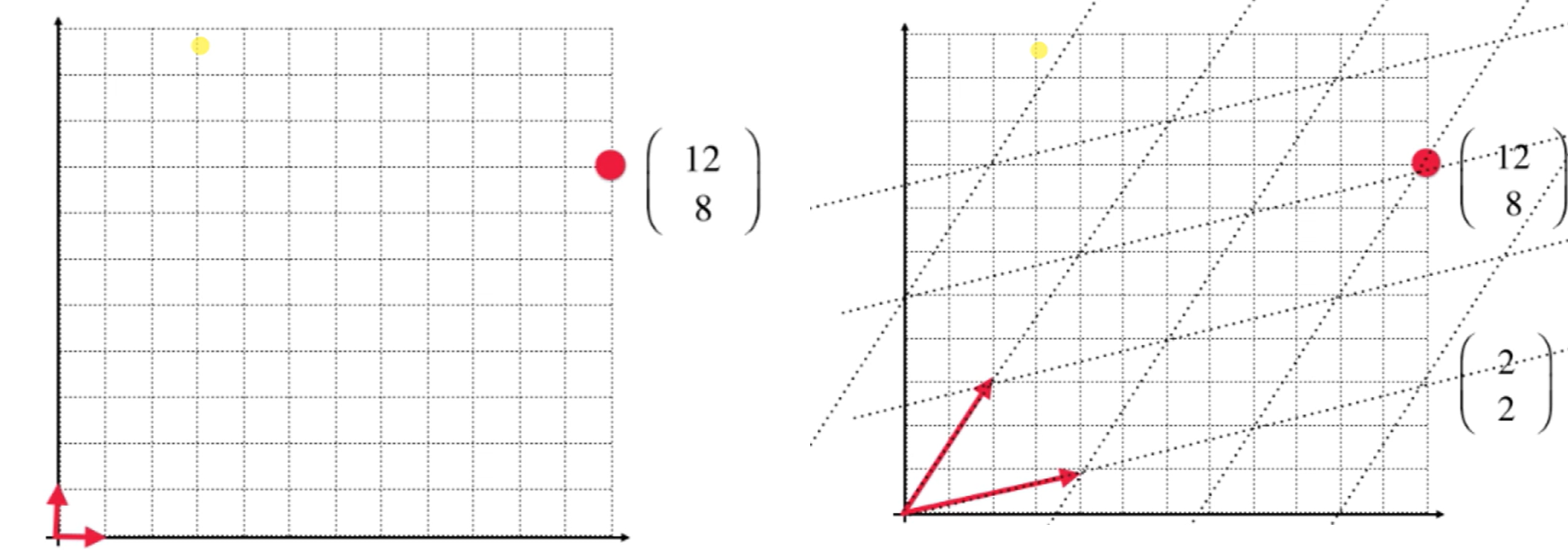
同样的一个二维平面空间中，我们使用了空间的两组基对应两个坐标系，一个点对应了两个坐标.

第一组基用矩阵表示：

(1001) \to (128)

第二组基用矩阵表示：

(4123) \to (22)

在n维空间，如果给定一组基，任何一个向量(或者是点)都可以表示成这组基的线性组合，且表示方法唯一.

对于(12,8)这个点：

e_{1} = (10)^{T}, e_{2} = (01)^{T} (128)^{T} = 12 (10)^{T} + 8 (01)^{T} = 12 e_{1} + 8 e_{2} u = (41)^{T}, v = (23)^{T} (128)^{T} = 2 (41)^{T} + 2 (23)^{T} = 2 u + 2 v

如果给定向量空间V中的一组基 $B = b_{1}, b_{2}, b_{3}, \dots b_{n}$ 以及V中的一个向量x,则x一定可以被这组基线性表示。假设：

x = c_{1} b_{1} + c_{2} b_{2} + c_{3} b_{3} + ... + + c_{n} b_{n}

则称x在这组基B下的坐标为 $(c_{1} c_{2} \dots c_{n})^{T}$ . 记为 $[x]_{B}$

举例：

ϵ = {e_{1}, e_{2}} [x]_{ϵ} = (128) B = {u, v} [x]_{B} = (22)

使用 $ϵ$ 这种坐标系是最常用的表示方法，这种基叫做标准基(Standard Basis),标准基对应的坐标系就是标准坐标系.

注意不要和标准正交基(Orthonormal)混淆,标准正交基是有无数组的，但标准基在n维空间中只对应一个，这一个基中所有的向量是有n-1个0，只有一个位置对应的元素为1.

其他坐标系与标准坐标系的转换

假设有一组基 $B = b_{1}, b_{2}, b_{3}, \dots b_{n}$ 设立矩阵 $P_{B} = (b_{1}, b_{2}, b_{3}, \dots b_{n})$ 在这组基下的一个向量 $[x]_{B}$ 有 $[x]_{ϵ} = P_{B} [x]_{B}$ .

比如上面的例子：

(4123) (22) = (128)

此时 $P_{B}$ 称为坐标转换矩阵.

因此任意坐标系向标准坐标系转换都有：

[x]_{ϵ} = P_{B} [x]_{B}

反过来标准坐标系向任意坐标系转换：

[x]_{B} = P_{B}^{- 1} [x]_{ϵ}

任意坐标系转换

现在考虑任意两个坐标系，它们之间如何相互转换？

假设有一组基 $B = b_{1}, b_{2}, b_{3}, \dots b_{n}$ ，另外一组基 $C = c_{1}, c_{2}, c_{3}, \dots c_{n}$ ,这两组基对应两个坐标系，这两个坐标系如何相互转换？假设B这组基下的一个向量 $[x]_{B}$ , 求 $[x]_{C}$ .

以标准坐标系为桥梁：

[x]_{ϵ} = P_{B} [x]_{B} [x]_{C} = P_{C}^{- 1} [x]_{ϵ} ↓ [x]_{C} = P_{C}^{- 1} P_{B} [x]_{B}

可以把两个矩阵合一起记为：

[x]_{C} = P_{B \to C} [x]_{B} P_{B \to C} = P_{C}^{- 1} P_{B}

同理反过来从C到B:

P_{C \to B} = P_{B}^{- 1} P_{C}

两个矩阵互为逆矩阵.

前面从任意坐标系向标准坐标系转换中的 $P_{B}$ 默认是：

P_{B} = ([b_{1}]_{ϵ} [b_{2}]_{ϵ} [b_{3}]_{ϵ} ... [b_{n}]_{ϵ})

我们知道这些基向量在我们要转到的坐标系即标准坐标系的表示.

假设有一组基 $B = b_{1}, b_{2}, b_{3}, \dots b_{n}$ ，另外一组基 $C = c_{1}, c_{2}, c_{3}, \dots c_{n}$ 如果我们知道 $([b_{1}]_{C} [b_{2}]_{C} [b_{3}]_{C} \dots [b_{n}]_{C})$ 在这组基下的一个向量 $[x]_{B}$ 求 $[x]_{C}$ .

那么就有：

P_{B \to C} = ([b_{1}]_{C} [b_{2}]_{C} [b_{3}]_{C} ... [b_{n}]_{C}) [x]_{C} = P_{B \to C} [x]_{B}

举个例子：

b_{1} = 1 c_{1} + 2 c_{2} b_{2} = 3 c_{1} + 4 c_{2} [b_{1}]_{C} = (1, 2)^{T} [b_{2}]_{C} = (3, 4)^{T} 在这组基下的一个向量 [x_{B}] = (2, 2)^{T} 求 [x]_{C}

显然：

P_{B \to C} = (1234) [x]_{C} = (1234) (22)

线性变换

通常数学中，变换是一个函数. 线性代数研究的是线性变换，一个变换T(x)称为线性变换，必须满足：

T (u + v) = T (u) + T (v) T (c u) = c T (u) c \in R

只探讨欧几里得空间，矩阵所表示的变换，均为线性变换.

为什么一个矩阵乘以一个向量被称为线性变换？

T (x) = A x

证明：

T (u + v) = A (u + v) = A u + A v = T (u) + T (v) T (c u) = A (c u) = c (A u) = c T (u)