线性代数
行列式
什么是行列式
行列式是方阵的一个属性. 矩阵可以表示一组向量，方阵表示n个n维向量.
下面的二维空间可以使用两个二维向量来作为空间的一组基，下面有三组基(三种颜色), 这三组基有什么不同？显然三组基对应的基向量具体都不一样，但是可以不可以只用一个数字表示这些向量组的不同？
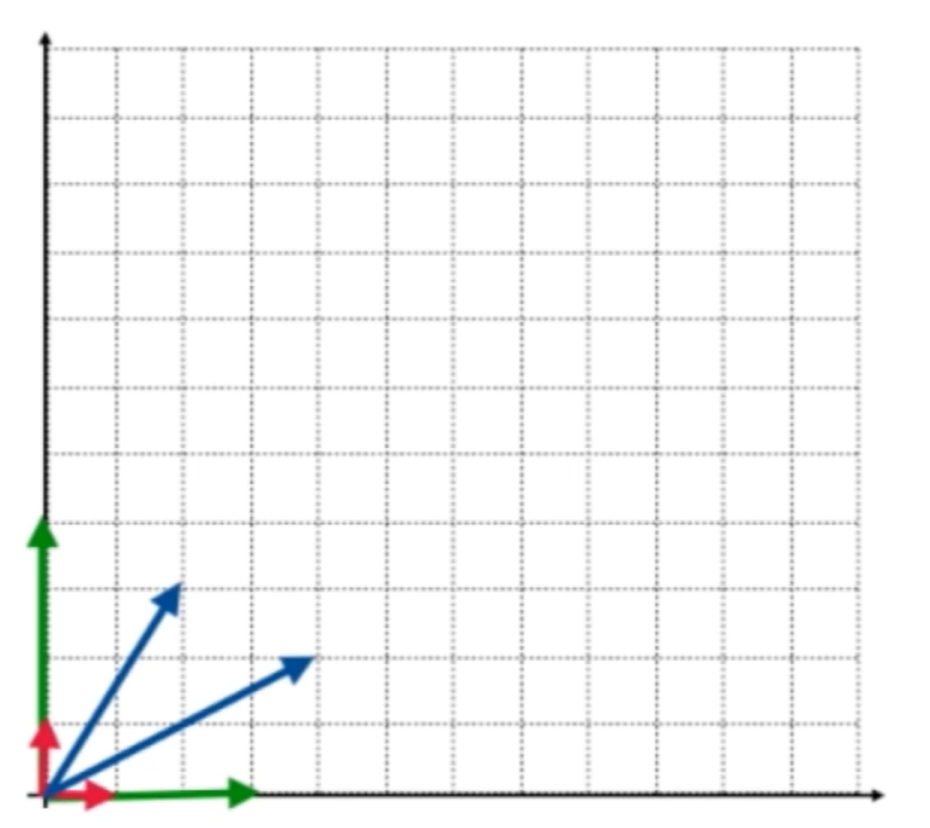
对于二维空间来说，每两个向量都组成了一个面积，比如红色的标准基面积为1，绿色的正交基面积为12，蓝色的基组成了一个平行四边形面积，这个面积的大小就可以一定程度刻画不同基的特征.
行列式就是描述n个n维向量所对应的n维体，对于二维空间来说就是面积，三维空间就组成了一个体.
行列式通常有下面两种表示方法：
$$
det\begin{pmatrix}
a &b\
c&d
\end{pmatrix} \quad
\begin{vmatrix}
a & b \
c & d
\end{vmatrix}
$$
行列式如何求呢？
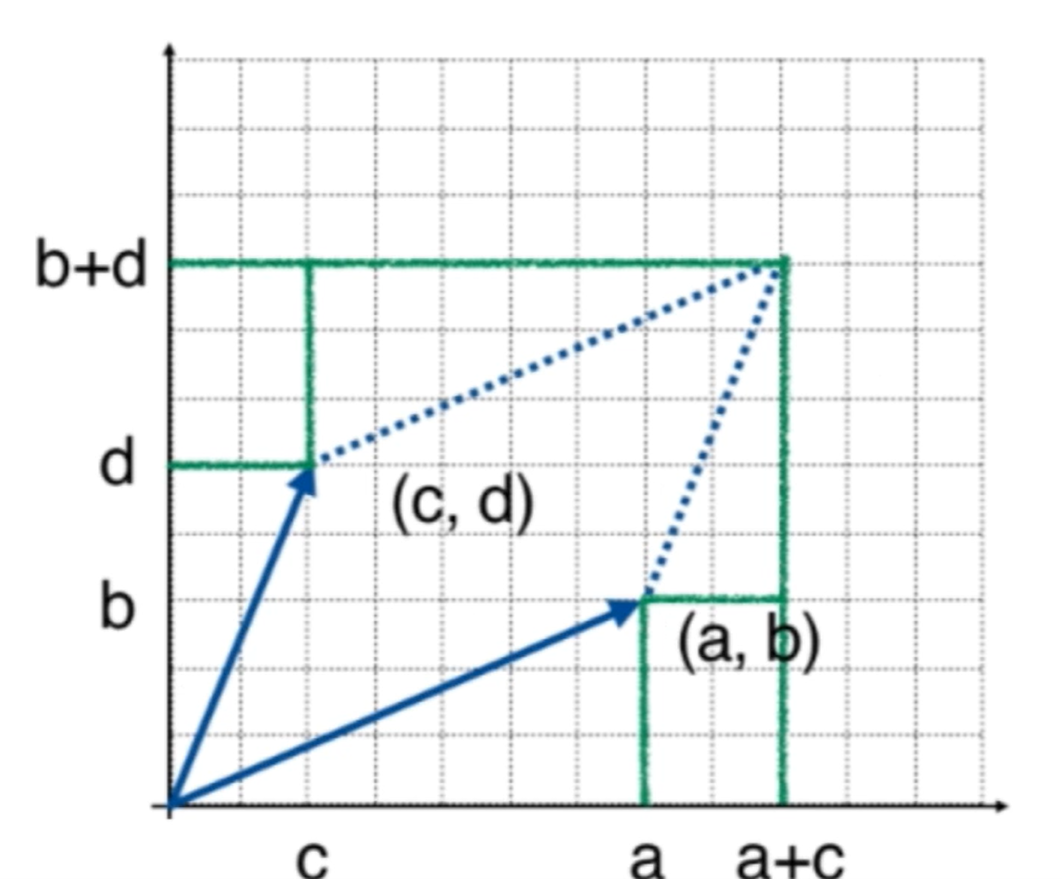
如上图所示，可以很自然表示出平行四边形面积：
$$
det\begin{pmatrix}
a &b\
c&d
\end{pmatrix}=(a+c)(b+d)-2bc-cd-ab\
=ad-bc
$$
因此对于二阶方阵，其行列式的值：
$$
\begin{vmatrix}
a & b \
c & d
\end{vmatrix}=ad-bc
$$
同时可以注意如果交换向量(a,b)和(c,d)的位置：
$$
\begin{vmatrix}
c & d\
a & b \
\end{vmatrix}=bc-ad
$$
所以行列式表示向量组在空间中形成的有向体积.（求出来的值可能正或负）
在三维及以上空间，体积的方向将变得极其复杂. 简单说，在行列式中，向量排列的顺序是有意义的. 交换两行，则行列式的值取反.
行列式的四大基本性质
行列式就是描述方阵的一个属性，对于这个方阵一行一行来看就是n个n维向量，这n个n维向量在n维空间中会构成一个n维体，这个n维体的有向体积就是行列式对应的值.
性质1：$det I=1$
性质2：交换行列式的两行，则行列式的值取反.
性质3：方阵的某一行乘以一个数k，则其对应的行列式也缩放了k倍.
$$
\begin{vmatrix}
ka & kb \
c & d
\end{vmatrix}=k\begin{vmatrix}
a & b \
c & d
\end{vmatrix}
$$
注意是某一行，而不是所有行. 矩阵的乘法是所有行. 因此$det(kA)=k^ndet(A)$
性质4：方阵的某一行加上一行数，则有：
$$
\begin{vmatrix}
a+a^, & b+b^, \
c & d
\end{vmatrix}=\begin{vmatrix}
a & b \
c & d
\end{vmatrix}+\begin{vmatrix}
a^, & b^, \
c & d
\end{vmatrix}
$$
行列式与矩阵的逆
根据上面的性质首先能得到一个推论：如果行列式的两行相同，则行列式的值为0.
$$
矩阵A交换两行后为A^,\
det(A)=-det(A^,)\
因为两行相同A=A^,\
det(A)=-det(A)\
det(A)=0
$$
推论2：如果行列式的一行是另一行的k倍，则行列式的值为0.
推论3：如果行列式有一行为0，则行列式的值为0.
推论4：如果行列式的一行是其他行的线性组合，则行列式的值为0.
行列式形成了一个向量组，如果这组向量线性相关，则行列式的值为0. 等价于 ——-矩阵不可逆.
如果这组向量线性无关，则行列式的值不为0. 等价于———–矩阵可逆.
$$
det(A)=0 \iff A不可逆\
det(A)\ne 0 \iff A可逆
$$
因此对于一个方阵A，可逆的等价命题如下：
计算行列式的算法
对于一个给定的行列式，具体应该怎么求呢？
性质5：如果一个行列式的一行加(减)零一行的k倍，行列式的值不变.
$$
\begin{vmatrix}
a & b &c \
d & e &f\
g & h & i
\end{vmatrix}=
\begin{vmatrix}
a & b &c \
d & e &f\
g-ka & h-kb & i-kc
\end{vmatrix}
$$
证明略(太简单了).
一个方阵的行列式的值等于其进行Gauss消元法后的结果（上三角矩阵U）, 等于其进行Gauss-Jordan消元法后的结果. 这里做的Gauss-Jordan消元法不要归一化,不能有行置换和列置换操作.
对角矩阵的行列式：
$$
\begin{vmatrix}
d_1 & 0&… &0 \
0&d_2&… & 0\
…&…&…&…\
0&0&…&d_n
\end{vmatrix}=d_1d_2…d_n \quad \begin{vmatrix}
d_1 & a_{12}&… &a_{1n} \
0&d_2&… & a_{2n}\
…&…&…&…\
0&0&…&d_n
\end{vmatrix}=d_1d_2…d_n \quad \begin{vmatrix}
d_1 & 0&… &0 \
a_{21}&d_2&… & 0\
…&…&…&…\
a_{n1}&a_{n2}&…&d_n
\end{vmatrix}=d_1d_2…d_n
$$
初等矩阵与行列式
行列式有这样一个性质：
$$
det(A.B)=det(A).det(B)\
$$
如果A或者B中的某一行和其他行线性相关，有:
$$
det(A.B)=0\
det(A) \quad or \quad det(B)=0
$$
如果A和B的所有行都线性无关，A和B都能表示成一系列初等矩阵的乘积.
初等矩阵是对单位矩阵进行初等行操作
假设矩阵A可以拆解为一系列初等矩阵：
$$
det(A.B)=det(E_k…E_2E_1B)
$$
如果E是单位矩阵的某一行乘以k,
$$
det(E)=k
$$
如果E是单位矩阵的某两行交换，
$$
det(E)=-1
$$
如果E是单位矩阵的某一行加(减)另一行的k倍，
$$
det(E)=1
$$
显然容易证明：
$$
det(E.B)=det(E).det(B)
$$
因此
$$
det(E_k…E_2E_1B)=det(E_k).det(E_{k-1})…det(E_2).det(E_1).det(B)\
det(A.B)=det(A).det(B)\
det(A.B)=det(E_k…E_2E_1B)=det(E_k).det(E_{k-1})…det(E_2).det(E_1).det(B)\
det(A)=det(E_k).det(E_{k-1})…det(E_2).det(E_1).det(I)\
得证det(A.B)=det(A).det(B)
$$
如果把B换成A的逆可得：
$$
det(A.B)=det(A).det(B)\
det(A.A^{-1})=det(A).det(A^{-1})\
det(I)=det(A).det(A^{-1})\
det(A).det(A^{-1})=1\
det(A^{-1})=\frac{1}{det(A)}
$$
这里$det(A)$ 在分母的位置，意味着如果要求出$A^{-1}$ 的行列式，$det(A)$ 不能为0. 侧面说明了如果矩阵A存在逆的话，$det(A)\ne0$ .
行式等于列式
对于行列式还有一个重要的性质：
$$
det(A)=det(A^T)
$$
证明:
$$
任意矩阵A可以分解称PLUP^,\
det(A)=det(PLUP^,)=det(P).det(L).det(U).det(P^，)\
det(A^T)=det((PLUP^,)^T)==det(P^{,T}).det(U^T).det(L^T).det(P^T)\得证
$$
前面的所有性质都是基于行，换成列一样存在.
行列式的一些话题
我们线性代数课本中行列式的代数表达式：
$$
\begin{vmatrix}
a_{11} & a_{12}&… &a_{1n} \
a_{21} & a_{22}&… &a_{2n} \
…&…&…&…\
a_{n1} & a_{n2}&… &a_{nn}
\end{vmatrix}=\sum_{i=1}^na_{1i}A_{1i}\
A_{1i}=(-1)^{i+1}M_{1i}
$$
其中$A_{1i}$ 是一个代数余子式.
课本中A的逆：
$$
A^{-1}=\frac{A^}{|A|}
$$
其中$A^$ 是伴随矩阵.
Crame法则：
$$
A\vec{x}=\vec{b}\
x_i=\frac{|A_i(b)|}{|A|}
$$
$A_i(b)$ 就是将A中的第i列换成b.