线性代数
特征值和特征向量
什么是特征值和特征向量
行列式本质上是方阵的一个属性, 而特征值和特征向量也是方阵的一个属性 . 其中的**“特征"描述的就是方阵的"特征”**, 更加准确的说对于一个矩阵既可以理解成变换又可以理解成空间,所谓的理解成空间是因为一个矩阵可以表示空间的基.
而特征值和特征向量更主要的是从变换的视角看方阵,当我们把方阵理解成一个变换,这个变换拥有一些特征. 这些特征将被特征值和特征向量表示出来.
具体看一个例子:
A = ( 4 − 2 1 1 ) ( 4 − 2 1 1 ) ( 1 4 ) = ( − 4 5 ) A=\begin{pmatrix}
4 & -2\\
1 & 1
\end{pmatrix}\\
\begin{pmatrix}
4 & -2\\
1 & 1
\end{pmatrix}\begin{pmatrix}
1\\
4
\end{pmatrix}=\begin{pmatrix}
-4\\
5
\end{pmatrix}
A = ( 4 1 − 2 1 ) ( 4 1 − 2 1 ) ( 1 4 ) = ( − 4 5 )
这个矩阵A可以理解为表示二维空间的一组基( 4 , 1 ) T , ( − 2 , 1 ) T (4,1)^T,(-2,1)^T ( 4 , 1 ) T , ( − 2 , 1 ) T
这个变换过程中我们比较关心一些特殊的向量:
( 4 − 2 1 1 ) ( 2 2 ) = ( 4 4 ) \begin{pmatrix}
4 & -2\\
1 & 1
\end{pmatrix}\begin{pmatrix}
2\\
2
\end{pmatrix}=\begin{pmatrix}
4\\
4
\end{pmatrix} \\
( 4 1 − 2 1 ) ( 2 2 ) = ( 4 4 )
( 4 − 2 1 1 ) ( 2 1 ) = ( 6 3 ) \begin{pmatrix}
4 & -2\\
1 & 1
\end{pmatrix}\begin{pmatrix}
2\\
1
\end{pmatrix}=\begin{pmatrix}
6\\
3
\end{pmatrix}
( 4 1 − 2 1 ) ( 2 1 ) = ( 6 3 )
这些向量通过矩阵A转换后,方向没有改变,结果是原来的常数倍 .
用数学式子表达:
A u ⃗ = λ u ⃗ A\vec{u}=\lambda\vec{u}
A u = λ u
其中λ \lambda λ (eigenvalue) ,u ⃗ \vec{u} u λ \lambda λ eigenvector .
具体有什么用? 后续可见
如何求解特征值和特征向量?观察上面式子,可知零向量肯定满足,是平凡解.
所以特征向量不考虑零向量. 但λ = 0 \lambda=0 λ = 0 A u ⃗ = 0 A\vec{u}=0 A u = 0 u ⃗ \vec{u} u λ = 0 \lambda=0 λ = 0
( A − λ I ) u ⃗ = 0 希望该方程有非零解,因此有 d e t ( A − λ I ) = 0 特征方程 (A-\lambda I)\vec{u}=0\\ 希望该方程有非零解,因此有\\
det(A-\lambda I)=0 \quad 特征方程
( A − λ I ) u = 0 希望该方程有非零解,因此有 d e t ( A − λ I ) = 0 特征方程
因此转换为了一个行列式的问题,行列式是求特征值和特征向量的基础. 这个方程也称为特征方程 .
∣ A − λ I ∣ = ∣ 4 − λ − 2 1 1 − λ ∣ = λ 2 − 5 λ + 6 = ( λ − 2 ) ( λ − 3 ) = 0 λ 1 = 2 , λ 2 = 3 λ 1 = 2 , ( A − 2 I ) u ⃗ = 0 ↓ u ⃗ = ( 1 1 ) T s λ 2 = 3 , ( A − 3 I ) u ⃗ = 0 ↓ u ⃗ = ( 2 1 ) T s |A-\lambda I|=
\left|
\begin{array}{ccc}
4-\lambda &-2 \\
1&1-\lambda \\
\end{array}
\right|\\=\lambda^2-5\lambda+6\\=(\lambda-2)(\lambda-3)=0\\
\lambda_1=2,\lambda_2=3\\
\lambda_1=2,(A-2I)\vec{u}=0\\
\downarrow\\
\vec{u}=(1\quad 1)^Ts \\
\lambda_2=3,(A-3I)\vec{u}=0\\
\downarrow\\
\vec{u}=(2\quad 1)^Ts
∣ A − λ I ∣ = 4 − λ 1 − 2 1 − λ = λ 2 − 5 λ + 6 = ( λ − 2 ) ( λ − 3 ) = 0 λ 1 = 2 , λ 2 = 3 λ 1 = 2 , ( A − 2 I ) u = 0 ↓ u = ( 1 1 ) T s λ 2 = 3 , ( A − 3 I ) u = 0 ↓ u = ( 2 1 ) T s
至此矩阵A的特征值以及对应的特征向量求出来了.
对应一个λ \lambda λ λ \lambda λ k ≠ 0 k\ne0 k = 0
特征向量组成了A − λ I A-\lambda I A − λ I
E λ = { O } ∪ { λ 的特征向量 } E_\lambda =\{O\}\cup\{\lambda 的特征向量\}
E λ = { O } ∪ { λ 的特征向量 }
E λ E_\lambda E λ λ \lambda λ
特征值和特征向量的性质
通过上面的讲解可知,对于方阵A:
多了新的一条等价命题,如果A可逆,则0不是A的特征值.
性质1:对角矩阵(上三角、下三角)的特征值是其对角线上的元素.(证明略)
性质2:若λ \lambda λ λ m \lambda ^m λ m A m A^m A m
数学归纳法 : m = 1 成立, A u ⃗ = λ u ⃗ 假设 m = k 成立, A k u ⃗ = λ k u ⃗ 当 m = k + 1 时 , A k + 1 u ⃗ = A . A k u ⃗ = λ k A u ⃗ = λ k λ u ⃗ = λ k + 1 u ⃗ 数学归纳法:m=1成立,A\vec{u}=\lambda\vec{u}\\
假设m=k成立,A^k\vec{u}=\lambda^k\vec{u}\\
当m=k+1时,A^{k+1}\vec{u}=A.A^k\vec{u}\\=\lambda^kA\vec{u}\\
=\lambda^k\lambda\vec{u}\\=\lambda^{k+1}\vec{u}
数学归纳法 : m = 1 成立, A u = λ u 假设 m = k 成立, A k u = λ k u 当 m = k + 1 时 , A k + 1 u = A . A k u = λ k A u = λ k λ u = λ k + 1 u
推论:若λ \lambda λ λ − 1 \lambda ^{-1} λ − 1 A − 1 A^{-1} A − 1
已知 A u ⃗ = λ u ⃗ A − 1 A u ⃗ = A − 1 λ u ⃗ u ⃗ = A − 1 λ u ⃗ A − 1 u ⃗ = λ − 1 u ⃗ 已知A\vec{u}=\lambda\vec{u}\\
A^{-1}A\vec{u}=A^{-1}\lambda\vec{u}\\
\vec{u}=A^{-1}\lambda\vec{u}\\
A^{-1}\vec{u}=\lambda^{-1}\vec{u}
已知 A u = λ u A − 1 A u = A − 1 λ u u = A − 1 λ u A − 1 u = λ − 1 u
性质3:如果矩阵A含有两个不同的特征值,则他们对应的特征向量线性无关.
A u ⃗ = λ 1 u ⃗ A v ⃗ = λ 2 v ⃗ 反证法 : 假设线性相关 u ⃗ = k v ⃗ , k ≠ 0 A u ⃗ = A ( k v ⃗ ) = k ( A v ⃗ ) λ 1 u ⃗ = k λ 2 v ⃗ λ 1 k v ⃗ = k λ 2 v ⃗ k ( λ 2 − λ 1 ) v ⃗ = 0 λ 2 = λ 1 , 矛盾 A\vec{u}=\lambda_1\vec{u} \quad A\vec{v}=\lambda_2\vec{v}\\
反证法:假设线性相关\\
\vec{u}=k\vec{v},k\ne0 \\
A\vec{u}=A(k\vec{v})=k(A\vec{v})\\
\lambda_1\vec{u}=k\lambda_2\vec{v}\\
\lambda_1k\vec{v}=k\lambda_2\vec{v}\\
k(\lambda_2-\lambda_1)\vec{v}=0\\
\lambda_2=\lambda_1,矛盾
A u = λ 1 u A v = λ 2 v 反证法 : 假设线性相关 u = k v , k = 0 A u = A ( k v ) = k ( A v ) λ 1 u = k λ 2 v λ 1 k v = k λ 2 v k ( λ 2 − λ 1 ) v = 0 λ 2 = λ 1 , 矛盾
代码求解特征值和特征向量示例:
1 2 3 4 5 6 7 8 9 10 11 import numpy as npfrom numpy.linalg import eigif __name__ == "__main__" : A1 = np.array([[4 ,-2 ],[1 ,1 ]]) eigenvalues, eigenvectors = eig(A1) print (eigenvalues) print (eigenvectors)
这个结果与上面例子求解的结果对应.
矩阵相似型
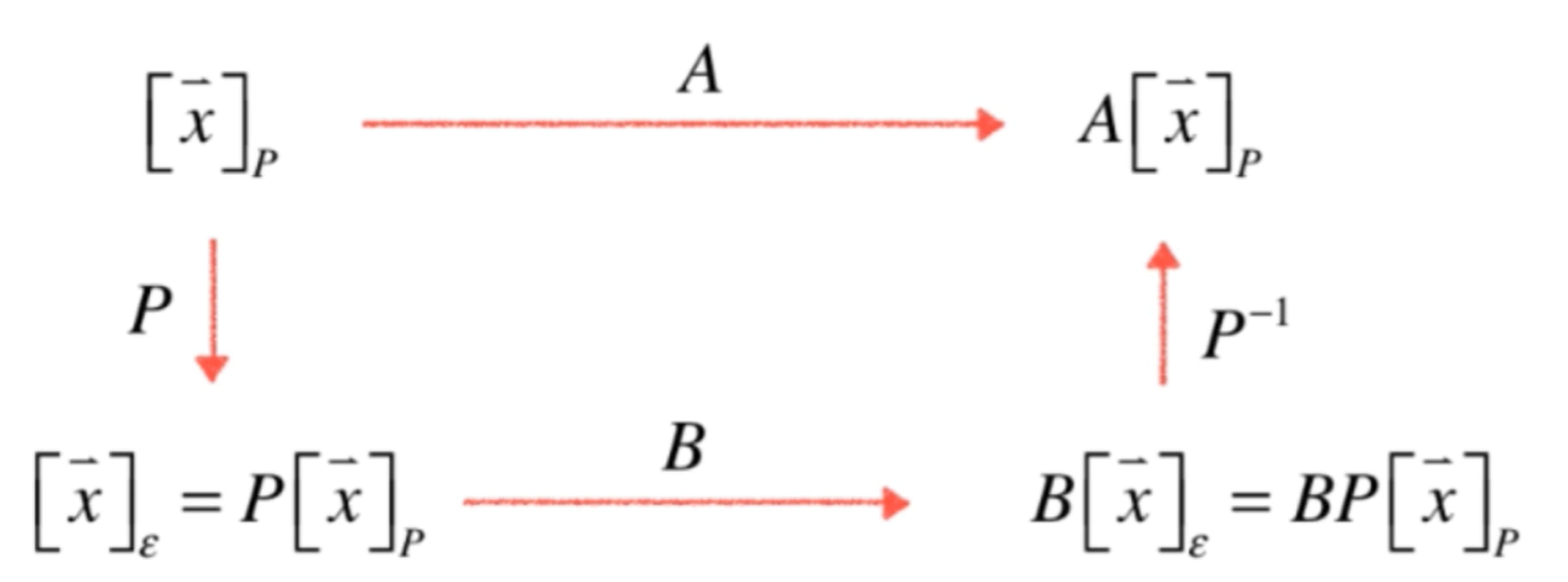
如果矩阵A, B满足A = P − 1 B P A=P^{-1}BP A = P − 1 BP
类比相似三角形. 矩阵相似本质上是从不同视角观察相同的内容.
如果P是一个坐标系,则A变换是在P坐标系下观察的B变换。
A [ x ⃗ ] p = P − 1 B P [ x ⃗ ] p A[\vec{x}]_p=P^{-1}BP[\vec{x}]_p
A [ x ] p = P − 1 BP [ x ] p
A和B本质是一个变换,只是观察的坐标系不同.
如果A和B相似,A和B的特征方程相同,特征值相同.
d e t ( A − λ I ) = d e t ( P − 1 B P − λ I ) = d e t ( P − 1 B P − λ P − 1 P ) = d e t ( P − 1 B P − P − 1 λ P ) = d e t ( P − 1 ( B − λ I ) P ) = d e t ( P − 1 ) d e t ( B − λ I ) d e t ( P ) = d e t ( B − λ I ) d e t ( P − 1 P ) = d e t ( B − λ I ) det(A-\lambda I)=det(P^{-1}BP-\lambda I)=det(P^{-1}BP-\lambda P^{-1}P)\\=
det(P^{-1}BP- P^{-1}\lambda P)\\
=det(P^{-1}(B-\lambda I) P)\\
=det(P^{-1})det(B-\lambda I)det(P)\\
=det(B-\lambda I)det(P^{-1}P)\\
=det(B-\lambda I)
d e t ( A − λ I ) = d e t ( P − 1 BP − λ I ) = d e t ( P − 1 BP − λ P − 1 P ) = d e t ( P − 1 BP − P − 1 λ P ) = d e t ( P − 1 ( B − λ I ) P ) = d e t ( P − 1 ) d e t ( B − λ I ) d e t ( P ) = d e t ( B − λ I ) d e t ( P − 1 P ) = d e t ( B − λ I )
这就是特征值和特征向量真正表征的”特征“,当我们把矩阵看作一个变换,这个变换不管从哪个角度哪个坐标系去看,它们都具有相同的特征. 既然已经知道对于一个变换可以从不同的角度去看,我们肯定希望找到一个最好的角度,用这个最好的角度去看它使得计算变换容易.
矩阵对角化
在P坐标系下观察B看到的是A,那么就可以变换P坐标系相应A就产生了变化,希望找到一个最好的A使得B这个变化非常简单. 这就是矩阵对角化所做的任务.
如果A有n个线性无关的特征向量,则A和某个D相似.
A = P D P − 1 A=PDP^{-1}
A = P D P − 1
D变换是P坐标系下观察到的A.
那么一个A如何分解成P D P − 1 PDP^{-1} P D P − 1
一个矩阵A如果可以被对角化的话:
D = ( λ 1 0 . . . 0 0 λ 2 . . . 0 . . . . . . . . . . . . 0 0 . . . λ n ) P = ( u 1 ⃗ u 2 ⃗ . . . u n ⃗ ) D=\begin{pmatrix}
\lambda_1&0&...&0 \\
0&\lambda_2&...&0 \\
...&...&...&... \\
0&0&...&\lambda_n \\
\end{pmatrix} \quad P=(\vec{u_1} \quad \vec{u_2}\quad ...\quad \vec{u_n})
D = λ 1 0 ... 0 0 λ 2 ... 0 ... ... ... ... 0 0 ... λ n P = ( u 1 u 2 ... u n )
D主对角线上的元素是矩阵A的特征值,P是对应的特征向量组成的特征向量矩阵 .
如果A有n个不相同的特征值,则A可以被对角化.
如果A没有n个不相同的特征值,A不一定不能被对角化.
对角化代码示例:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 import numpy as npfrom numpy.linalg import eig, invfrom LA.LinearSystem import rankfrom LA.Matrix import Matrixdef diagonalzie (A ): assert A.ndim ==2 assert A.shape[0 ] == A.shape[1 ] eigvalues, eigvectors = eig(A) P = eigvectors if rank(Matrix(P.tolist())) != A.shape[0 ]: print ("Matrix can not be diagonalized" ) return None , None , None D = np.diag(eigvalues) Pinv = inv(P) return P, D, Pinv if __name__ == "__main__" : A1 = np.array([[4 ,-2 ], [1 ,1 ]]) P1, D1, Pinv1 = diagonalzie(A1) print (P1) print (D1) print (Pinv1) print (P1.dot(D1).dot(Pinv1))
对角化应用
求解矩阵的幂:
A 2 = P D P − 1 P D P − 1 = P D 2 P − 1 A 3 = P D P − 1 P D P − 1 P D P − 1 = P D 3 P − 1 A n = P D n P − 1 D = ( λ 1 0 . . . 0 0 λ 2 . . . 0 . . . . . . . . . . . . 0 0 . . . λ n ) D 2 = ( λ 1 2 0 . . . 0 0 λ 2 2 . . . 0 . . . . . . . . . . . . 0 0 . . . λ n 2 ) D n = ( λ 1 n 0 . . . 0 0 λ 2 n . . . 0 . . . . . . . . . . . . 0 0 . . . λ n n ) A^2=PDP^{-1}PDP^{-1}=PD^2P^{-1}\\
A^3=PDP^{-1}PDP^{-1}PDP^{-1}=PD^3P^{-1}\\
A^n=PD^nP^{-1}\\
D=\begin{pmatrix}
\lambda_1&0&...&0 \\
0&\lambda_2&...&0 \\
...&...&...&... \\
0&0&...&\lambda_n \\
\end{pmatrix} \quad D^2=\begin{pmatrix}
\lambda_1^2&0&...&0 \\
0&\lambda_2^2&...&0 \\
...&...&...&... \\
0&0&...&\lambda_n^2 \\
\end{pmatrix} \quad D^n=\begin{pmatrix}
\lambda_1^n&0&...&0 \\
0&\lambda_2^n&...&0 \\
...&...&...&... \\
0&0&...&\lambda_n^n \\
\end{pmatrix}
A 2 = P D P − 1 P D P − 1 = P D 2 P − 1 A 3 = P D P − 1 P D P − 1 P D P − 1 = P D 3 P − 1 A n = P D n P − 1 D = λ 1 0 ... 0 0 λ 2 ... 0 ... ... ... ... 0 0 ... λ n D 2 = λ 1 2 0 ... 0 0 λ 2 2 ... 0 ... ... ... ... 0 0 ... λ n 2 D n = λ 1 n 0 ... 0 0 λ 2 n ... 0 ... ... ... ... 0 0 ... λ n n
这样计算矩阵的幂只用到了两次矩阵乘法.
为什么关心矩阵的幂?
大量问题的形式都跟矩阵的幂有关:
u ⃗ k = A k u ⃗ 0 \vec{u}_k=A^k\vec{u}_0
u k = A k u 0