Linear Algebra(12):对称矩阵和SVD

线性代数

对称矩阵和矩阵的SVD分解

完美的对称矩阵

对称矩阵即矩阵的所有元素关于主对角线对称：

(1001) (1223) 1 - 1 5 - 1 2 π 5 π 3

用数学表达对称矩阵：

A = A^{T}

为什么说对称矩阵是完美的？对称矩阵的特征值一定是实数（证略）. 对称矩阵的多重特征值，其对应的特征空间的维度一定等于重数.对称矩阵的几何重数等于代数重数. 对称矩阵一定有n个线性无关的特征向量.

因此对称矩阵一定可以被对角化.

正交对角化

对称矩阵的所有不同的特征值对应的特征向量互相垂直.

假设矩阵A的两个特征向量v1,v2对应不同的特征值 $λ_{1}, λ_{2}$

证明 v_{1} . v_{2} = 0 (λ_{1} v_{1}) . v_{2} = (λ_{1} v_{1})^{T} v_{2} = (A v_{1})^{T} v_{2} = v_{1}^{T} A^{T} v_{2} = v_{1}^{T} A v_{2} = v_{1}^{T} λ_{2} v_{2} = λ_{2} v_{1}^{T} v_{2} = λ_{2} v_{1} . v_{2} = 0 (λ_{1} - λ_{2}) (v_{1} . v_{2}) = 0 ↓ (v_{1} . v_{2}) = 0

对称矩阵一定可以被对角化：

A = P D P^{- 1}

如果A是对称矩阵，

A = Q D Q^{- 1} A = Q D Q^{T}

此时的Q是标准正交矩阵，这个式子就是把A进行了正交对角化.

正交对角化就是在对角化的基础上保证P是一个标准正交矩阵，写成字母Q.

如果A可以被正交对角化，则A一定是对称矩阵.

A = Q D Q^{T} A^{T} = (Q D Q^{T})^{T} = Q D^{T} Q^{T} = Q D Q^{T} = A 得证

因此：

A 是对称矩阵 ⟺ A 可以被正交对角化 A = Q D Q^{T}

这个结论也叫做谱定理.

奇异值

前面讨论的特征值、特征向量、相似型、对角化、对称矩阵、正交对角化都是基于方阵的。但实际处理的数据很多是非方阵，对于每一个非方阵来说，我们都可以找到一个对称矩阵和它对应.

如果A是一个m*n的矩阵，则 $A^{T} A$ 是一个n*n 的方阵,且对称.

第 i 行第 j 列元素 : A^{T} 第 i 行点乘 A 第 j 列 相当于 A 第 i 列点乘 A 第 j 列 第 j 行第 i 列元素 : A^{T} 第 j 行点乘 A 第 i 列 相当于 A 第 j 列点乘 A 第 i 列

因此 $A^{T} A$ 是对称矩阵.

$A^{T} A$ 可以被正交对角化，拥有n个实数特征值 $λ_{1}, \dots, λ_{i}$ ，n个互相垂直的标准特征向量 $v_{1}, \dots, v_{i}$ .

下面式子：

∣∣ A v_{i} ∣ ∣^{2} = (A v_{i}) . (A v_{i}) = (A v_{i})^{T} . (A v_{i}) = v_{i}^{T} (A^{T} A v_{i}) = v_{i}^{T} (λ_{i} v_{i}) = λ_{i} v_{i}^{T} v_{i} = λ_{i} ∣∣ v_{i} ∣ ∣^{2} = λ_{i}

这个式子说明每一个 $λ_{i}$ 都可以表示成一个上面向量模的平方，因此 $A^{T} A$ 的特征值>=0 .将 $σ_{i} = λ_{i}$ 称为奇异值(Singular Value).

奇异值就是 $A v_{i}$ 的长度.

${A v_{i}}$ 是A的列空间的一组正交基， $λ_{i} \neq = 0$ .

证明正交性：

(A v_{i}) . (A v_{j}) = (A v_{i})^{T} (A v_{j}) = v_{i}^{T} A^{T} A v_{j} = v_{i}^{T} (A^{T} A v_{j}) = v_{i}^{T} (λ_{j} v_{j}) = λ_{j} v_{i}^{T} v_{j} = λ_{j} (v_{i} . v_{j}) = 0

证明 ${A v_{i}}$ 是A的列空间的一组基：

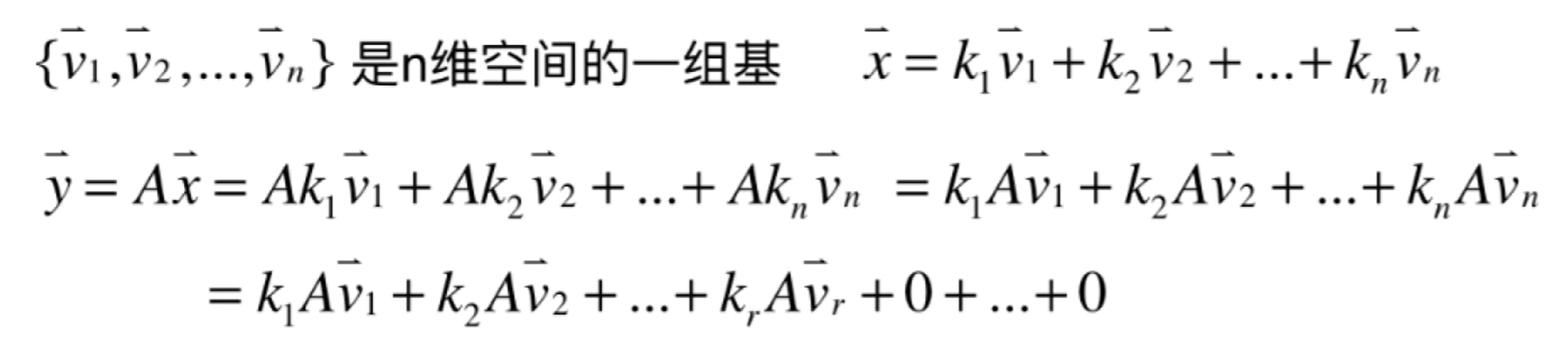
如果A有r个不为零的奇异值， ${A v_{1}, A v_{2}, \dots, A v_{r}}$ 是A的列空间的一组正交基. A的列空间维度为r,rank(A)=r.

${\frac{A v _{1}}{σ _{1}}, \frac{A v _{2}}{σ _{2}}, \dots, \frac{A v _{r}}{σ _{r}}}$ 是A的列空间的一组标准正交基.

通常把奇异值从大到小排序，把 $σ_{i} = 0$ 的奇异值丢掉.

奇异值的SVD分解

矩阵的SVD分解-Singular Value Decomposition , 即矩阵的奇异值分解. 对任意形状的矩阵都适用.

A = U \sum V^{T}

如果A是m*n的矩阵，U是m*m 的矩阵； $\sum$ 是m*n 的矩阵(奇异值矩阵)；V是n*n的矩阵.

V是 $A A^{T}$ 的特征向量矩阵进行标准化，U和V都是标准正交矩阵.

证明：

A V = U \sum v_{i} 是 A^{T} A 的标准特征向量

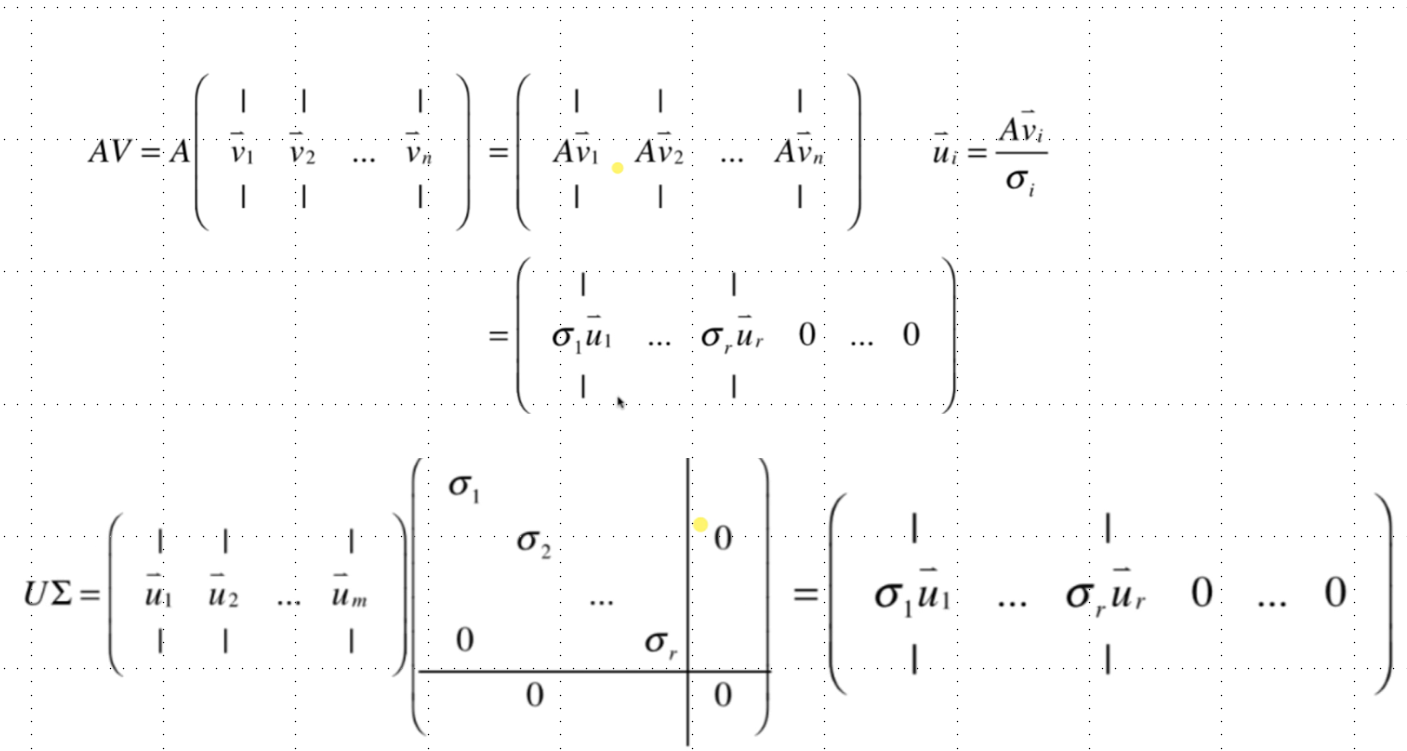
具体流程：

求解 $A^{T} A$ 的特征值和特征向量
非零特征值开根后(奇异值)得到m*n的 $\sum$ ,奇异值从大到小排序
特征向量标准化后得到n*n的V
$u_{i} = \frac{A v _{i}}{σ _{i}}$ 在经过Gram-Schmidt扩展得到m*m的U

SVD代码示例：

import numpy as np
from scipy.linalg import svd


if __name__ == "__main__":

    A = np.array([[1, 2],
                  [3, 4],
                  [5, 6]])
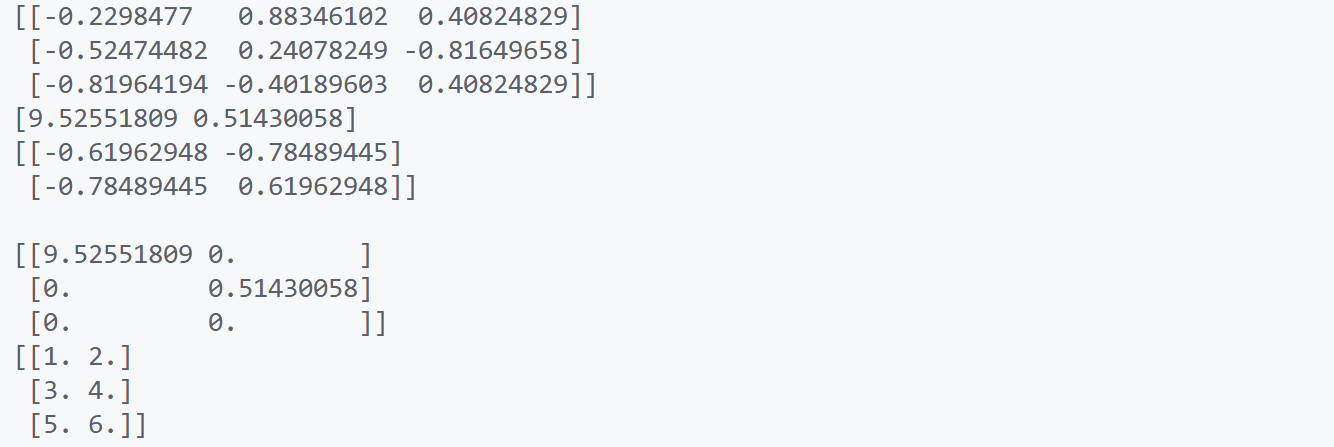
    U, s, VT = svd(A)
    print(U)
    print(s)
    print(VT)
    print()


    Sigma = np.zeros(A.shape)
    for i in range(len(s)):
        Sigma[i][i] = s[i]
    print(Sigma)
    print(U.dot(Sigma).dot(VT))

SVD分解的应用

第一个应用是将矩阵A看作是一个变换. 如果A是一个m*n矩阵，A只能对n维向量做变换.

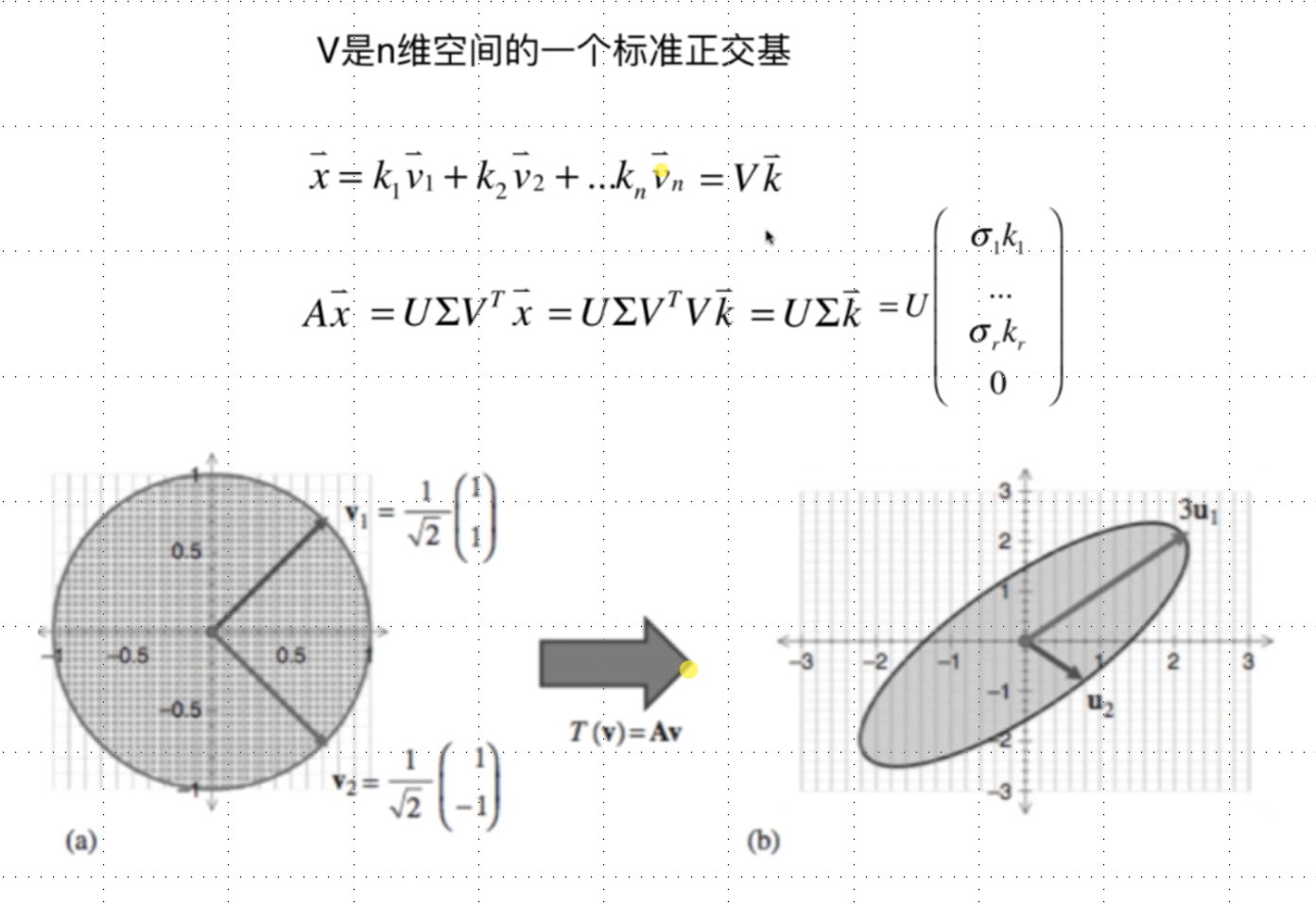
列视角看待A,把矩阵A看成一片数据:

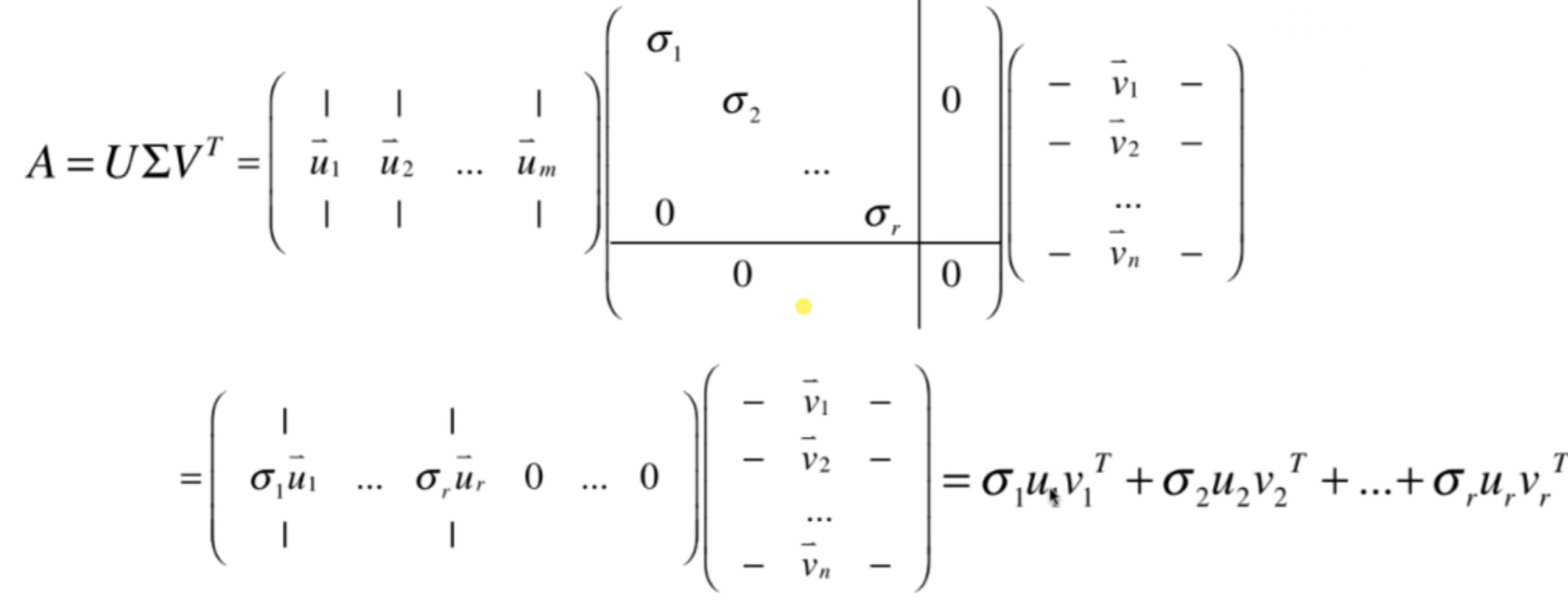
可以用来压缩、去噪、降维.